Теорема 4. Ранг матрицы треугольного (ступенчатого) вида равен числу ненулевых строк матрицы

Аналогичная теорема справедлива для вектор–столбцов матрицы.

Пример 1. Ранг тождественного отображения : X ⁿ→ Y ^m (при любых соотношениях между n и m) равен n: r () = r (E _n) = n (см. пример 1, п. 2.).

Пример 2. Ранг дифференциального оператора 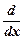: P _n-1→ → P _n-2 равен (n -1): 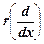= r (D _(n-1)хn))= r (D _(n-1))= n -1 (см. пример 3, п. 2).

Пример 3. Найдем ранг матрицы

.

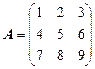Приведем матрицу к эквивалентной матрице треугольного вида следующими элементарными преобразованиями (обозначения аналогичны обозначениям преобразований с определителями, см. §2, п. 2):

,

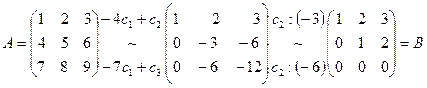r (A) = r (B) = 2 (по строкам). Значит, в матрице А только две вектор–строки (любые) линейно независимы.

Установим этот факт, оперируя со столбцами

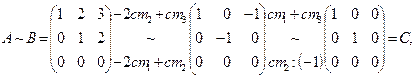отсюда r (A) = r (B) = r (С) = 2 (по столбцам). Очевидно, в матрице С только 2 вектора (строки или столбцы): =(1, 0, 0), 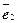=(0, 1, 0) линейно независимы. Это же справедливо и для матрицы А. Заметим, например, что 3-й вектор–столбец есть линейная комбинация первых двух: ст ₃ = 2· ст ₂– ст ₁.

Пример 4. Докажем, что векторы = (4; 1), 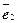= (-2; 3) образуют базис пространства А² (см. § 1, п. 5, пример 6).

Составим матрицу А, записав, например, векторы строками и найдем ее ранг:

.

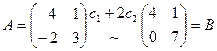Отсюда r (A) = r (B) = 2 и имеем два линейно независимых вектора, которые в 2-мерном пространстве образуют базис.

Date: 2015-12-10; view: 339; Нарушение авторских прав