Определители

Каждой квадратной матрице n –го порядка А можно поставить в соответствие некоторое число – определитель n –го порядка (│А│, D (A), detA, ∆(A), ∆ - обозначения), который вычисляется по определенному правилу. Далее мы сформулируем это правило – «разложение определителя по любой строке (столбцу)» – с помощью индукции.

Пусть n =2.

.

Например, =2×1-4×(-3)=2+12=14.

Пусть n =3.

Минором M _ij, соответствующим элементу a _ij матрицы А, называется определитель, получающийся из матрицы А после вычеркивания i –ой строки и j –го столбца, на пересечении которых стоит элемент a _ij; i =1, 2, …, n; j =1, 2, …, n:

Алгебраическим дополнением A _ij элемента a _ij матрицы А называется величина:

A _ij = (–1)^{i+ j}× M _ij, например: А ₁₁= М ₁₁, А ₁₂=- М ₁₂, ….

Если сумма индексов четная, то множитель перед минором дает знак «+», если нечетная «–». Распределение знаков иллюстрируется матрицей

.

Определение 2.2. Правило вычисления определителя по любой строке (столбцу) матрицы:

1 вариант (по 1-й строке):

│ А │= а ₁₁ А ₁₁+ а ₁₂ А ₁₂+ а ₁₃ А ₁₃ = а ₁₁ М ₁₁– а ₁₂ М ₁₂+ а ₁₃ М ₁₃;

2 вариант (по 2–му столбцу):

│ А │= а ₂₁ А ₂₁+ а ₂₂ А ₂₂+ а ₂₃ А ₂₃ = - а ₂₁ М ₂₁+ а ₂₂ М ₂₂– а ₁₃ М ₁₃.

Аналогичным образом определяется и вычисляется определитель n -го порядка: сводится к вычислению n определителей (n –1)-го порядка.

Пример 1.

а). Разложим определитель по 1-ой строке:

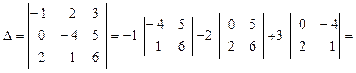
= (-1)(-24-5)-2(0-10)+3(0+8)=29+20+24=73.

б). Разложим определитель по 2-ой строке:

=-4(-6-6)-5(-1-4)=73.

Свойства определителей (на примерах определителей 2-го порядка).

Величина определителя:

1) не меняется, если матрицу A транспонировать, то есть строки заменить соответствующими столбцами: А *

2) меняет знак, если у него переменить местами две строки (столбца):

3) умножается на число k, если элементы строки (столбца) умножить на k:

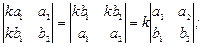
то есть общий множитель в строке (столбце) можно выносить за знак определителя;

4) равна нулю, если элементы любого столбца (строки) равны нулю:

0× b ₂-0× b ₁= 0;

5) равна нулю, если имеются равные строки (столбцы):

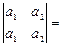a ₁× a ₂- a ₂× a ₂= 0;

6) не изменится, если к элементам любой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на число k:

,

(к I-й строке (столбцу) прибавить 2-ю строку (столбец), умноженную на число k – рекомендуем кратко записывать так: k×с ₂+ с ₁ (k × сТ ₂+ сТ ₁);

7) равна произведению элементов стоящих на диагонали, если матрица диагональная или треугольного вида:

(убедитесь в этом, разложив определитель по 1-му столбцу).

8). Определитель от произведения А × В квадратных матриц А, В равен произведению определителей от каждой матрицы А, В: │ А × В │=│ А │×│ В │.

Рекомендуем проверить все свойства определителя на конкретных матрицах.

Date: 2015-12-10; view: 308; Нарушение авторских прав