Координаты вектора

Определение 5. Векторы , , …, из векторного пространства Х называются линейно независимыми, если равенство

a₁ + a₂ +…+ a_n = (6)

имеет место только когда все числа a₁ = a₂ =… a_n = 0. В противном случае, то есть когда равенство выполняется при существовании чисел из a₁, a₂, …, a_n не равных одновременно нулю, векторы , , …, называются линейно зависимыми.

Если векторы , , …, линейно зависимы, то один из векторов может быть представлен в виде линейной комбинации остальных векторов. Например, если в (6) a₂ ¹0, то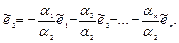

Определение 6. Пространство Х называется конечномерным, а число n – размерностью (рангом, числом измерений) этого пространства, если в Х существует n линейно независимых векторов, в то время как любые n +1 векторов из Х линейно зависимы. Если же в пространстве можно найти линейно независимую систему из любого числа векторов, то пространство называется бесконечномерным.

В этой главе мы будем иметь дело в основном с конечномерными пространствами Xⁿ. Размерность («dimension») обозначается dim X.

Определение 7. Система из n линейно независимых заданных в определенном порядке векторов , , …, в n – мерном пространстве Хⁿ называется базисом этого пространства.

Пусть – произвольный вектор этого пространства. Тогда векторы , , , …, линейно зависимы (ибо число их равно n +1) и справедливо равенство a₀ + a₁ + a₂ +…+ a_n = , где, по крайней мере, a₀ ¹0, так как векторы , , …, не могут быть связаны линейной зависимостью. Поэтому:

= х₁ + х₂ +…+ x_n (7)

где числа х_i = , i =1, 2, …, n, однозначно определяются заданием вектора и базиса , , …, . В самом деле, если наряду с (7) имеется другое разложение вектора по базису:

= х₁ ¢ + х₂ ¢ +…+ х_n¢ (7¢)

то вычитая почленно (7) из (7¢), получим (х₁¢ – х₁) +(х₂¢ – х₂) +…+(x_n¢ – x_n) , откуда в силу линейной независимости векторов базиса следует х₁¢ – х₁ = х₂¢ – х₂ =…= x_n¢-x_n =0, то есть х₁¢=х₁, х₂¢=х₂, …, x_n¢=x_n.

Числа х₁, х₂, …, х_n в (7) называются координатами вектора в базисе , , …, , что кратко записывается так: (х₁, х₂, …, х_n) в базисе , , …, .

Слагаемые в (7) называют компонентами вектора .

Может возникнуть вопрос, нельзя ли, например, в трехмерном пространстве найти базис из меньшего числа векторов. Оказывается, что нет – для любого векторного пространства Xⁿ, имеющего базис из n элементов, и любой другой базис этого пространства состоит из n элементов (доказательство не приводим).

Пример 1. Докажем, что ортонормированные векторы , , …, 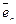арифметического пространства Aⁿ линейно независимы, а значит, в n – мерном пространстве образуют базис. Размерность пространства Aⁿ, а значит и Rⁿ, равна n.

Согласно определению равенства векторов, векторное равенство (6) в нашем случае имеет вид a₁ + a₂ +…+ a_n 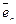= и эквивалентно в координатной форме следующей системе скалярных равенств: a₁ = 0, a₂ = 0, … a_n = 0, что доказывает линейную независимость векторов , , …, 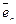и наше утверждение, так как любой вектор = (х₁, х₂, …, х_n) пространства Aⁿ есть линейная комбинация векторов , , …, : .

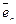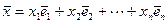Пример 2. Рассмотрим систему векторов = 3 х +5, = 2 х -1, порождающую пространство Р₁ = { a + b } = { a (3 x +5)+ b (2 x –1)} = {(3 a +2 b) x +(5 a – b)} = { ax + b }, где переменная х Î R, a = 3 a +2 b, b = 5 a – b; a, b Î R.

Это линейное пространство многочленов не выше 1–ой степени. Любой элемент - многочлен вида р (х) = aх + b, элемент нуль = 0× х +0.

Покажем, что векторы , линейно независимы (геометрически – это графики двух пересекающихся прямых). Равенство (6) имеет вид: a₁ + a₂ = или a₁ (3 x +5)+ a₂ (2 x –1) = 0× х +0, (3 a +2 b) x +(5 a – b)} = 0× х +0, что эквивалентно системе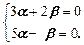

Отсюда b = 5 a; подставляя в первое уравнение, имеем 3 a +10 a = 0, a = 0, а значит и b = 0.

Из определения пространства Р₁ очевидно, что любой вектор = aх + b есть линейная комбинация линейно независимых векторов и ,см. (7):

aх + b = x₁ + x₂ (8).

Значит, векторы , образуют базис пространства Р₁ и его размерность равна 2.

Расписывая равенство (8): (3 х₁ +2 х₂) х +(5 х₁ – х₂)= aх + b, получим систему уравнений которая имеет единственное решение: - координаты вектора в базисе , .

Конкретно, вектор = х +6 будет иметь координаты (1, -1), вектор = 3 х +5 - координаты (1, 0) в базисе = 3 х +5, = 2 х –1.

Пример 3. Пусть независимые переменные х, у и коэффициенты С, А, В принимают числовые значения из R. Рассмотрим множество П₂ выражений вида С + Ах + Ву, обращающихся в нуль при х = 2, у = -1 (другими словами, являются решениями систем уравнений вида С + Ах + Ву =0: П₂ ={ С + Ах + Ву: C +2× A –1× B =0}.

Геометрически на плоскости z = 0 (ХОУ)это есть пучок прямых, проходящих через точку (2, -1).

Множество П ₂ - векторное пространство, так как умножая такие выражения на произвольные числа и складывая их (то есть образуя линейные комбинации), мы будем получать выражения такого же типа. Элемент нуль имеет вид = 0 + 0× х + 0× у.

Покажем, что выражения (элементы, вектора) = х –2, = у +1 образуют базис в пространстве П ₂, а значит размерность его равна 2.

Согласно равенству (6) будем иметь: a₁ + a₂ = или подробно: a₁ (х –2)+ a₂ (у +1)= 0+0× х +0× у, (a₂ –2 a₁)+ a₁х + a₂у = 0+0× х +0×у. Приравнивая соответствующие коэффициенты, получим систему уравнений решение которой есть a₁ = 0, a₂ = 0, что доказывает линейную независимость векторов , . Покажем, что произвольный элемент = (х, у)Î П₂ есть линейная комбинация векторов , : (х, у) = С + Ах + Ву = С + А (х –2+2)+ В (у +1–1) = = С + А (х –2)+ В (у +1)+2 А – В = А (х –2)+ В (у +1)+ С +2 А – В = А + В . Значит, векторы , образуют базис пространства П ₂ и справедливо разложение по базису произвольного вектора (см. (7)): (х, у) º С + Ах + Ву =А +В . В этом базисе вектор имеет координаты (А; В).

Например, выражение 3 х +5 у –1 имеет координаты (3; 5) и справедливо разложение по базису 3 х +5 у -1 = 3 + 5 .

Однако заметим, например, что выражение 2 х +3 у –1 не принадлежит векторному пространству П ₂.

Пример 4. (Аналогично примеру 1 показывает существование «хорошего» базиса).

Пусть значения переменной х Î R. Система из (n +1)–го элемента = 1, = х, = х²,..., = xⁿ порождает векторное пространство многочленов не выше n –ой степени

Р_n = { a₀ + a₁ + a₂ +…+ a_n } ={ a₀ + a₁x + a₂x² +…+ a_nxⁿ }, где произвольные числа a_i Î R, i =1, …, n. Нулевой элемент пространства P_n:

= 0+0× х +0× х² +…+0× хⁿ.

Элементы , , …, линейно независимы, так как равенство a₁ + a₂ + … + a_n+1 = или a₁ + a₂x + a₃x² + … + a_n+1xⁿ = 0+0× х +0× х² + … +0× xⁿ справедливо только тогда, когда a₁ = a₂ = a₃ = … = a_n+1 = 0.

Любой вектор (многочлен n –й степени) есть линейная комбинация линейно независимых векторов: (х) = a₀ + a₁x + a₂x₂ +…+ + a_nxⁿ = a₀ + a₁ + a₂ +…+ a_n , значит, векторы , , …, образуют базис пространства Р_n, и вектор имеет координаты (a₀, a₁, a₂,…, a_n). Размерность пространства P_n равна n +1.

Пример 5. Покажем, что векторы = х² +2 х –3, = х² –5 х +4, = 3 х² +5 х –8 линейно зависимы и не могут образовать базис пространства Р₂ (см. пример 4), размерность которого 3.

Согласно (6) распишем равенство a₁ + a₂ + a₃ = .

Приравнивая коэффициенты при одинаковых степенях х, получим однородную систему уравнений, , которая, кроме нулевого решения a ₁ = a₂ = a₃ = 0, имеет и другие, например решение (a₁; a₂; a₃)=(20; 1; -7), что доказывает наше утверждение.

Пример 6. Докажите, что векторы =(4; 1), =(-2; 3), образуют базис пространства А². Найдите координаты вектора =(-1; 5) в этом базисе.

Так как пространство А² размерности 2, то достаточно доказать линейную независимость векторов , . Распишем согласно (6) равенство a₁ + a₂ = . Имеем: a₁ (4; 1)+ a₂ (-2; 3) = (0; 0) или Однородная система имеет единственное нулевое решение a₁ = 0, a₂ = 0, так как определитель системы не равен нулю.

Это означает, что векторы , линейно независимы и образуют базис в А², то есть любой вектор можно однозначно представить (см.(7)) в виде: х ₁ + х ₂ = .

Расписывая равенство покоординатно, для определения координат х₁, х₂ получим систему: Отсюда получим: х₁ =0,5, х₂ =1,5; вектор имеет координаты = (0,5; 1,5) в базисе из векторов , .

Пример 7. Векторное пространство всех многочленов P _∞={ р (х): р (х)= a₀ + a₁х + a₂х² +… a_nxⁿ, a_i Î R, i =0, 1, … n; n – произвольное неотрицательное целое число} бесконечномерное, так как всегда можно найти линейно независимую систему, состоящую из любого числа элементов, например, 1, х, х², …, хⁿ, n - произвольное натуральное число (см. пример 4, где n – фиксировано), что и требовалось доказать.

Пример 8. По аналогии с пространством Аⁿ (п. 1) рассмотрим пространство А^∞ = { x: x = (a₁, a₂, … a_n, …), a_i Î R }, элементами которого являются всевозможные упорядоченные бесконечные наборы вещественных чисел a₁, a₂, …. Аналогичным образом определим операции над элементами. Пространство А^∞ уже будет бесконечномерным. Если предположить, что бесконечномерные пространства изоморфны пространству А^∞ (см. п. 6), то нетрудно понять, что между бесконечномерными и конечномерными пространствами есть много общего.

Date: 2015-12-10; view: 437; Нарушение авторских прав