Матрица преобразования координат. Обратная матрица

1). Рассмотрим линейное преобразование координат вектора =(х ₁, х ₂, …, х _n) в координаты вектора 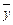=(у ₁, у ₂, …, у _m):

, (2)

заданное матрицей из пространства L _Am´n:

(3)

где коэффициенты a _ijÎ R. Рассмотрим два пространства: n –мерное X ⁿ и m –мерное Y ^m. Выберем в X ⁿ некоторый базис , , …, и в Y ^m некоторый базис , , …, . Тогда преобразование (2) дает возможность в соответствие каждому вектору

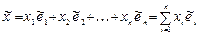
из X ⁿ поставить вектор из Y ^m, координаты которого вычисляются по формулам (2). Значит, преобразование заданное матрицей А, определяет некоторое отображение , относящее вектору вектор , то есть : X ⁿ→ Y ^m. Нетрудно видеть, что оператор обладает свойством линейности:

(a + β ') = a + β ' (, 'Î X ⁿ, a, β Î R).

Итак, каждая матрица A= A _m´nÎ L _m´n размера m´n при заданных базисах порождает линейное отображение : X ⁿ → Y ^m, Î (X ⁿ, Y ^m).

Замечание. Линейное преобразование (2) в матричной форме можно записать так: = А · , где · означает умножение матрицы А на вектор–столбец =[ x ₁, x ₂, …, x _n]; =[ y ₁, y ₂, …, y _m] – тоже вектор–столбец. В векторном равенстве = справа стоит обозначение образа элемента при действии отображения на элемент , Î Y ^m, слева () – его краткое обозначение или равный ему другой элемент пространства Y ^m.

2). Докажем обратное, т.е. что для произвольного линейного оператора , отображающего X ⁿ в Y ^m, и произвольных базисов , , …, в X ⁿ и , , …, в Y ^m существует матрица A _mхn, и составленное при помощи этой матрицы линейное преобразование (2) ( = A _mхn· ) выражает координаты преобразованного вектора = через координаты исходного вектора .

Линейное отображение : X ⁿ→ Y ^m можно однозначно определить заданием образов элементов базиса при этом отображении.

Действительно, применим оператор к базисному вектору , и координаты вектора Î Y ^m в базисе , , …, обозначим через а _1k, а _2k, …, a _mk, k =1, 2, …, n:

(4).

Отсюда видно, что линейное отображение однозначно определяется коэффициентами a _ji, которые образуют матрицу отображения :

(5).

Пусть = х ₁ + х ₂ +…+ x _n = . Используя линейность оператора , меняя порядок суммирования, получим: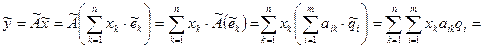

, где , i =1, 2, …, m. Это дает преобразование (2) соответственно в матричной форме:

, (6)

с матрицей преобразования координат

, (7)

т.е. матрица преобразования координат А _mхn (3) есть транспонированная матрица (5) отображения .

Итак, установлено взаимно однозначное соответствие J между векторным равенством и матричным равенством , между оператором и матрицей преобразования координат А, коэффициенты которой зависят от рассматриваемых базисов пространств, между пространствами (X ⁿ, Y ^m) и L _Amxn.

Установим теперь, что отображение J сохраняет линейные операции, то есть, является линейным, а значит изоморфизмом.

Пусть линейным операторам , Î L (X ⁿ, Y ^m) соответствуют матрицы A _mxn= A, B _mxn= B. Тогда линейному оператору = α + β (α, β Î R) по аналогии с выше проведенными выкладками соответствует матрица преобразования координат F = α А + βB, что и требовалось установить.

Далее покажем, что произведению операторов = (см. п. 3.1), где : X ⁿ→ Y ^r, : Y ^r→ Z ^m, : X ⁿ→ Z ^m, отвечает матрица C = B·A.

Действительно векторным равенствам

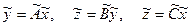
будут соответствовать матричные равенства

,

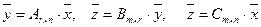где - столбцы координат векторов в некоторых базисах. Отсюда для любого , соответственно любого , находим и в силу произвольности заключаем, что верно равенство (см. п. 2.1.):

.

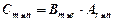Пусть имеем изоморфизм : Х ⁿ → Y ⁿ, тогда существует обратное отображение и справедливы векторные равенства (п.3.1):

= , = или ( ) = , ( ) = для " Î Х ⁿ, " Î Y ⁿ или = , = ,

где , тождественные (единичные) отображения соответственно пространств Х ⁿ, Yⁿ в себя.

Отображениям в некоторых базисах соответствуют матрицы преобразования координат: ↔ А, ↔ А ^-1, ↔ Е, ↔ E, и справедливы матричные равенства: = А ∙ , = А ^-1 или А ^-1 А = , АА ^-1 = или А ^-1 А = Е, АА ^-1= Е; Е – единичная матрица.

Определение. Квадратная матрица А ^-1 называется обратной к квадратной матрице А, если справедливы равенства: А ∙ А ^-1 = А ^-1∙ А = Е.

Пример 1. Обозначим через линейное отображение (тождественное), при котором = (: Х ⁿ→ X ⁿ – отображение пространства в себя). Найдем отвечающую матрицу преобразования координат.

Пусть – базис пространства X ⁿ. Тогда последовательно имеем:

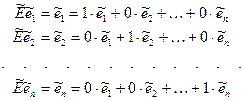
Матрицей преобразования координат (совпадает с матрицей отображения ) будет единичная матрица Е.

Линейное преобразование вида l , l Î R, называется гомотетией с коэффициентом l. Ему отвечает матрица lЕ. Преобразование координат векторов в базисе запишется равенством: = lЕ = l .

Пример 2. Пусть Х = R, Y = R, и мы рассматриваем линейные отображения у = х на множестве вещественных чисел как векторном пространстве (естественно это уже «обычные» функции у = f (x) с областью определения и областью значений R).

Какие же функции в этом случае можно назвать линейными? Для характеристики отображения f (функции) достаточно указать в какие элементы переводятся элементы базиса пространства R. В одномерном пространстве R за базис может быть принято число 1, =1, так как любое число х может быть представлено как х = х∙1 = х ∙ (разложение по базису).

Пусть f ()= k - некоторое фиксированное число, тогда f () = k ∙ (см.4), матрица А _1х1 = (k), и мы имеем согласно (6): у = kх. Геометрически такая функция изображается прямой, проходящей через начало координат, то есть это действительно линейная функция. Пример 3. Рассмотрим отображение (оператор дифференцирования), которое каждому многочлену p (x)= a ₀+ a ₁ x + a ₂ x ²+…+ a _n-2 x ^n-2+ a _n-1 x ^n-1 из пространства Р _n-1 (см. пример 4, п. 1.3.) ставит в соответствие по формуле:

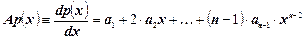
многочлен из пространства P _n-2. Оператор дифференцирования является линейным оператором, так как

,

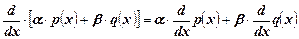где p (x), q (x)Î P _n-1, a, β Î R.

В пространствах X = X ⁿ≡ P _n-1, Y = Y ^m≡ X ^n-1≡ P _n-2 выберем базисы из степеней х:

= x ⁰= 1, = x, = x ², …, = x ^n-1;

= 1, = x, = x ², … = x ^n-2.

Пользуясь формулами (4):

...............

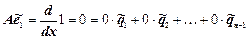
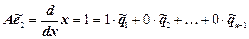
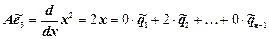
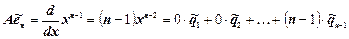
Построим матрицу преобразования координат (7), (3)

.

Запишем в указанных базисах матричную формулу вычислений координат вектора–столбца = (b ₀, b ₁, b ₂, …, b _n-2)Î A ^n-1↔ X ^n-1= = P _n-2 по координатам вектора–столбца = (a ₀, a ₁, a ₂, …, a _n-1) ↔ ↔ p (x)Î P _n-1:

= D ∙ .

Такой подход позволяет свести операцию дифференцирования в конечномерных пространствах (в тех, где она имеет смысл) к обычному умножению числовых матриц и, естественно, к полной автоматизации вычислений на компьютере.

Пример 4. Рассмотрим линейное преобразование , заданное формулой (2) , где матрица А = описывает удельные нормы расхода компонентов сырья , (i = 1,2,…,m:сахар, патока, …, шоколад) для приготовления единицы (1 грамма) вида продукта (j=1,2,…,n: конфеты «мишка на севере», «каракум»,…, «белочка»), тогда вектор -количественный план производства. Линейность преобразовани я будет означать:

1) аддитивность: 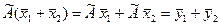-расход сырья для суммы двух планов производства (например,для двух рабочих дней) равен сумме расходов сырья для осуществления каждого плана (сумме расходов сырья за каждый день);

2) однородность: -расходы сырья для выполнения плана ( равны расходам по выполнению плана , умноженным в раз.

Очевидно, если план производства и матрица А заданы, то затраты сырья определяются по формуле 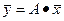, используя ЭВМ и соответствующие программы.

Обратная задача, , когда известны запасы сырья и удельные нормы расходов –матрица А, а план производства вектор неизвестен, рассматривается в параграфе 4 этой главы.

Date: 2015-12-10; view: 745; Нарушение авторских прав