Абстрактные векторные (линейные) пространства

Многие типы математических объектов обладают общим для всех них свойством: операции сложения их элементов, природа которых нас не интересует, и умножения элемента на число, не выводят нас за пределы исходного множества.

Приведем примеры таких множеств.

1) Множество действительных чисел R = R¹.

2) Множество векторов арифметического пространства Аⁿ.

3) Множество функций определенных (непрерывных или дифференцируемых) на интервале (0; 1). Под суммой двух функций f (x) и q (x) понимается функция, принимающая в точке х значение f (x)+ q (x); под произведением функции f (x) на число λ понимается функция, которая в точке х принимает значение λ·f (x).

Если бы мы занялись исследованием алгебраических свойств одного из приведенных конкретных примеров, то невольно использовали и такие свойства, которые в других случаях не имеют места. Именно с целью проведения исследования в общем случае вводится понятие абстрактного векторного пространства.

Для произведения вычислений в этих пространствах заранее определяются основные свойства операций, которые высказываются в виде аксиом. Для умножения элементов пространства на числа и операций с ними от области чисел требуется выполнимость четырех арифметических действий, говорят, потребуется числовое поле. Числовое поле образуют, например, множество рациональных чисел Q или множество вещественных чисел R.

Определение 3. Назовем множество Х абстрактным векторным (линейным) пространством над числовым полем R, если во множестве определены операция сложения: для любых двух элементов 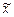, Î Х определен третий элемент из Х, который обозначается + , и операция умножения на число: для любого элемента 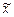Î Х и любого числа a Î R определен элемент a из Х, удовлетворяющие следующим аксиомам: для " , , Î Х, a, b Î R:

1. + = + ;

2. ( + )+ = +( + );

3. Существует элемент (нулевой) в X такой, что произведение числа 0 на любой элемент Î Х равно элементу :0× = ;

4. 1· = ;

5. a ×(b × )=(a × b)× ;

6. (a + b)× = a × х + b × ;

7. a ×( + )= a + a .

Из этих аксиом можно получить следующие следствия. Для " Î Х справедливо + = ; это действительно так: + =1· +0· =(1+0) =1· = .

Существует единственный противоположный элемент

=(-1) такой, что +()=1× +(-1)× =(1–1)× =0× = . Если предположить, что существует другой противоположный элемент такой, что + = , то, прибавляя к обеим частям равенства вектор , получим: ( + )+()= +(), ( – )+ = , + = , = .

Элементы из Х называют также векторами, а элементы поля R – скалярами.

В первый момент кажется, что аксиом очень много. Однако не следует забывать, что чем меньше свойств выполняется по предположению, тем меньше можно свойств (теорем) доказать, основываясь на них. Достаточно глубокие результаты можно получить (для всех сразу векторных пространств!) лишь в том случае, если мы потребуем выполнения достаточно большого количества аксиом.

Заметим, что 4-я аксиома позволяет исключить из рассмотрения такое «векторное пространство», в котором произведение любого вектора на произвольное число равнялось бы нулевому вектору.

Пример. Превратим множество столов с прямоугольными крышками белого цвета шириной в один метр и произвольной длины в линейное пространство. Для этого договоримся, что под суммой двух столов будем понимать стол с крышкой, длина которой равна сумме длин крышек столов и Операцию умножения числа 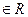на любой стол определим следующим образом: длина стола умножается в раз, цвет крышки стола не меняется при и меняется на черный при 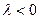. Нулевым элементом будет стол с крышкой нулевой длины, т. е. без крышки; естественно . Противоположный элемент -стол с черной крышкой –таков, что .

Все аксиомы линейного пространства естественным образом выполняются. (Какова размерность этого пространства?; см. ниже п.5).

Date: 2015-12-10; view: 1764; Нарушение авторских прав