Линейные отображения (операторы)

1. Основные понятия и определения.

Линейное пространство L (X, Y).

В геометрии исключительно важную роль играют преобразования: сдвиг, поворот, растяжение и другие (на плоскости или в трехмерном пространстве), обладающие тем свойством, что сумму векторов они переводят в сумму их образов, а произведение вектора на число a - в произведение образа вектора на a. Обычно их называют линейными отображениями, они играют ведущую роль среди всех отображений.

Определение. Пусть Х и Y – векторные пространства над числовым полем R. Поставим в соответствие каждому вектору Î Х некоторый вектор у из пространства Y, который обозначим через А , говорят, что задано отображение (оператор) , отображающее Х в Y (обозначают: : Х → Y или = ). Если для любых , из Х и " a Î R выполняются равенства

(a ) = a ( ), (свойство однородности)

( + )= + , (свойство аддитивности)

то отображение называют линейным отображением (линейным оператором).

Можно объединить оба равенства в эквивалентное им одно:

(a + β ) = a + β , a, β Î R.

Линейные отображения : Х → Y, В: Х → Y мы назовем равными, если для любого Î Х А = Вх.

Элементы вида 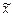образуют подпространство пространства Y, называемое пространством образов при отображении : Х → Y, и обозначают символом (Х) = { : Î Х }, (Х) Ì Y.

Если (Х) = Y, то называется отображением Х на Y.

При линейном отображении нуль–элемент пространства Х обязательно переходит в – нуль–элемент пространства Y: = ( – ) = – = , но возможно, и другие элементы ≠ отображаются в нуль–элемент .

Поэтому, определим множество прообразов элемента , которое назовем ядром линейного отображения : Х → Y и обозначим:

Н ≡ () = { Î Х: = Î Y }, Н Ì Х.

Ядро Н также является (линейным) подпространством пространства Х (докажите самостоятельно).

Если линейное отображение не взаимно однозначно (Н ≠ { }), то при 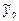= всякий вектор , для которого 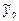= , имеет вид = + , где – некоторый вектор ядра Н. Множество векторов ={ = + : Î H } называется многообразием (гиперплоскостью) параллельным подпространству Н (по-другому, сдвигом подпространства Н на вектор ); при = , = Н. При ≠ , не есть подпространство.

Размерность ядра Н называют дефектом отображения А и обозначают d () или : d () = dimH, (d (A) ≤ dimX).

Если ядро Н = { } (d (A)=0) состоит только из нуль-элемента , то отображение : Х → (Х) – взаимно однозначное отображение Х на пространство образов (Х). Существует обратное (тоже линейное) отображение : (Х) → Х или = , = ( = , " Î Х).

Если дополнительно предположим, что (Х) = Y, то имеем линейное взаимно однозначное отображение пространства Х на пространство Y, то есть изоморфизм, который устанавливает изоморфное соответствие между пространствами Х и Y (: Х ↔ Y) (см. п. 6). Естественно, в этом случае = , " Î X, обратно, = , " Î Y и справедливы равенства: ( ) = , ( ) = или = , = , где , -тождественные (единичные) операторы: = , " ÎX, = , " ÎY.

Проиллюстрируем сказанное на рисунке:

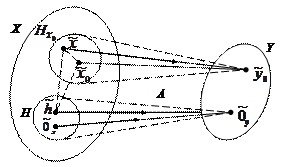а) Линейное отображение А из Х в Y.

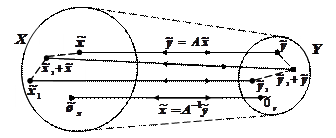б) Изоморфизм Х и Y.

Рисунок 2.

Образы n линейно независимых элементов пространства Х при линейном отображении в пространство Y в общем случае не будут линейно независимыми; но справедлива следующая

Теорема 1. Если в пространстве Y образы (), (), …, () линейно независимы, то соответствующие r элементов , , …, пространства Х линейно независимы в Х.

Естественно, справедлива эквивалентная ей (обратная противоположной)

Теорема 2. Если , , …, линейно зависимы в Х, то их образы , , …, при отображении также линейно зависимы.

Действительно, пусть, например, вектор есть линейная комбинация остальных векторов: = a ₂ , …, a ₃ + … + a _r , a _iÎ R, тогда в силу линейности отображения , имеем: = a ₂ + a ₃ +…+ a _r , что означает линейную зависимость векторов–образов.

Следовательно, справедлива следующая теорема.

Теорема 3. Если линейное отображение : Х ⁿ→ Y, то подпространство (Х ⁿ) пространства Y имеет размерность, не большую n:

dim A (X ⁿ)≤ n.

В случае : Х → Y ^m подпространство (Х)Ì Y имеет размерность не большую m: dim (X) ≤ m; в частности, при (Х) = Y ^m размерность dim (X)= m.

Определение. Рангом отображения : Х → Y называют размерность пространства образов (Х) и обозначают r (): r ()= dim (X).

Очевидно, если линейное отображение : X ⁿ→ Y ^m, то справедливо неравенство: r () = dim (X ⁿ) ≤ min { m; n }, то есть ранг отображения А меньше или равен наименьшему из чисел m, n; отображает Х ⁿ на некоторое r - мерное подпространство (Х ⁿ) пространства Y ^m (r ≤ min { m, n }).

Без доказательства сформулируем следующую теорему.

Теорема 4. Если линейное отображение : Х → Y, то справедлива формула: r ()+ d () = dimX (ранг + дефект = размерность Х).

В частности, при : Х ⁿ→ Y имеем r ()+ d () = n.

Над линейными отображениями можно производить некоторые операции: их можно умножать на число l, можно складывать, в определенных случаях перемножать.

Сформулируем определения этих операций.

Если : Х → Y и l Î R, то l обозначает линейное отображение, при котором для любого Î Х (l × ) = l .

Так как Î Y, то l × = (l × ) Î Y, значит, l : Х → Y. Покажем, что отображение l – линейное. Имеем для " , Î Х, a, β Î R: l (a + β ) = ( (a + β )) = l (a + β ) = la + lβ =

= a (l ) + β (l ) , что доказывает сказанное.

Если : Х → Y, Х → Z, то + обозначает линейное отображение, при котором для " Î Х

( + ) = + .

Аналогично предыдущему легко убедиться, что + является линейным отображением и + : Х → Y.

Если : Х → Y, : Y → Z, то (произведение отображений, операторов или композиция) обозначает линейное отображение, при котором для " Î Х ( ) = ( ).

Покажем, что : Х → Y. Действительно, если Î Х, то Î Y и, так как : Y → Z, то ( )=( ) Î Z. Нетрудно показать, что является линейным отображением.

Очевидно, что умножение линейных отображений не коммутативно.

Можно показать, достаточно лишь проверить выполнение аксиом, что совокупность линейных отображений (операторов) : X → Y относительно определенных выше операций сложения и умножения на число сами образуют векторное (линейное) пространство, которое мы обозначим (X, Y) ≡ L(X, Y).

Нуль–элементом этого пространства является нулевой оператор θ, переводящий элементы пространства Х в нуль–элемент пространства Y.

Отметим, что если существуют произведения и , то существуют и произведения ( ) и ( ) , причем ( ) = ( ) (ассоциативность произведения).

Date: 2015-12-10; view: 505; Нарушение авторских прав