Линейные комбинации векторов. Подпространство

Под линейными комбинациями векторов , , …, понимаются векторы вида

a₁ + a₂ + …+ a_n ,

где a₁, a₂, … a_n – произвольные числа из R.

Если все числа a_i (i =1, 2,…, n) равны 0, то имеем тривиальную линейную комбинацию – нулевой вектор .

Определение 4. Пусть в векторном пространстве Х имеется множество векторов Х₀ Ì Х, удовлетворяющее следующим условиям:

1) " , Î Х₀ Þ + Î Х₀;

2) " Î Х₀, " a Î R Þ a Î Х₀,

тогда множество Х₀ называется подпространством (линейным многообразием) векторного пространства Х.

Если в векторном пространстве выбрать некоторое множество векторов, то всевозможные конечные линейные комбинации векторов образуют некоторое подпространство векторного пространства, которое называется подпространством, порожденным этим множеством векторов.

Если подпространство, порожденное некоторым множеством элементов векторного пространства, совпадает с самим пространством, то такое множество называется системой, порождающей пространство. В этом случае любой вектор пространства может быть представлен линейной комбинацией системы векторов.

Примером является система векторов , , …, , 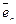порождающая пространство Aⁿ и представляющая любой вектор Î Aⁿ в виде линейной комбинации: = х₁ + х₂ +…+ x_n 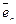, где x_i – числа.

Заметим, что вектор – нуль всегда принадлежит подпространству.

Date: 2015-12-10; view: 343; Нарушение авторских прав