Доказательство. 1. Пусть V1 и V2 - j-инвариантные подпро­странства, то есть jV1 Í V1, jV2 Í V2

1. Пусть V₁ и V₂ - j -инвариантные подпро­странства, то есть jV₁ Í V₁, jV₂ Í V₂. Тогда j(V₁ + V₂) = jV₁ + jV₂ Í V₁ + V₂.

2. Пусть V₁ и V₂ - j -инвариантные подпро­странства, и

хÎ V₁ ∩ V₂. Тогда хÎ V₁, хÎV₂, и j хÎ V₁,j хÎV₂, так что

j хÎ V₁ ∩ V₂.

3. "хÎ V имеем j хÎ V Þ j ²х = j(j х)Î V, …, j ⁿхÎ V, и так как V – подпространство, то

f(j)х = a₀ id_L x +a₁j x + …+ a_nj ⁿхÎ V Þ V - f(j)- инвари- антное подпространство.

ÿ

Рассмотрим, как существование у линейного оператора j инвариантного подпространства связано со свойствами его матрицы [ j ].

Пусть j: Lⁿ ® Lⁿ - линейный оператор, Lⁿ É L^m - j- инва- риантное подпространство (1£ m< n), {е₁,…, е_m} – базис в L^m. Дополним базис L^m до базиса е = {е₁,…, е_m, е_m+1,…, е_n} всего пространства Lⁿ. В базисе е оператор j имеет полураспав­шуюся матрицу:

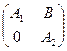[ ] = , (16.1)

где А₁ – (m´ m)- матрица, А₂ – (n-m)´(n- m)- матрица, 0 – ну-­

левая (n-m)´ m- матрица. В самом деле, "j =1,…,m j е_j Î L^m,

то есть j е_j =a_1jе₁+…+ a_mjе_m + 0е_m+1+…+0е_n.

Обратно, если в некотором базисе е ={е₁,…, е_m, е_m+1,…_,е_n}

пространства Lⁿ оператор j имеет полураспавшуюся мат­рицу вида (16.1), то <е₁,…, е_m >= L^m - j- инвариантное подпространство. В самом деле, "j =1,…,m jе_jÎ L^m (так как jе_j раскладывается только по векторам е₁,…, е_m) Þ " х Î L^m, х= a₁е₁+…+ a_mе_m, имеем j х = a₁j е₁+…+ a_mj е_mÎ L^m.

Выводы.

1. Л.о. j имеет нетривиальное инвариантное подпространство Û в Lⁿ $ базис, в котором матрица [ j ] - полураспавшаяся.

2. Подпространство L^m - j- инвариантно Û для любого (достаточно, для некоторого) базиса {е₁,…, е_m } в L^m j е_j Î L^m "j =1,…,m.

Пусть j: L® L - линейный оператор, LÉV - j- инвариант-

ное подпространство. Определим отображение j|_V: V® V так: "xÎ V пусть по определению j|_V(x)= j x.

Упражнение. Доказать, что j|_V – линейный оператор.

Определение. Линейный оператор j|_V: V® V называется ограничением j на V, или оператором, индуцированным на инвариантном подпространстве V линейным оператором j.

Очевидно, j и j|_V отличаются лишь областью определе­ния, и на подпространстве V имеет место равенство j =j|_V.

Замечание. Очевидно, линейное отображение j|_V будет линейным оператором Û V - инвариантное подпространство.

Легко видеть, что для примера 2 j|_V1 =id, j|_V2 =0, а для примера 3 j|_V1 – поворот плоскости, j|_V2 = id. В случае же оператора с матрицей (16.1), очевидно, в базисе {е₁,…, е_m} [ 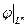] = А₁.

Прямая сумма инвариантных подпространств.

Пусть j: Lⁿ ® Lⁿ - линейный оператор, Lⁿ=L₁ Å L₂ - пря­мая сумма j- инвариантных подпространств L₁ и L₂ ,

е¢ ={е₁,…,е_m} – базис в L₁, е¢¢ ={е_m+1,…,е_n} – базис в L₂, dimL₁= m, dimL₂= n - m. Тогда е = {е₁,…,е_m,е_m+1,…_,е_n} – ба­зис всего пространства Lⁿ, и в этом базисе из инвариантности L₁ матрица [ j ] имеет вид (16.1). Но мы можем утверждать и большее. Так как L₂ – также j- инвариантно, то "j =m+1,…,n j е_jÎ L₂, то есть j е_j = 0е₁+…+0е_m + a _m+1,j е_m+1+…+a_nj е_n Þ в матрице (16.1) В = 0, то есть

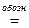[ ] = А₁ ∔ А₂ - (16.2)

распавшаяся или блочно-диагональная матрица. Здесь А₁ – квадратная матрица порядка m, А₂ - квадратная матрица по­рядка n – m, А₁ = , А₂ = .

Обратно, если в некотором базисе е матрица [ ] имеет

вид (16.2), то Lⁿ=L₁ Å L₂ - прямая сумма j- инвариантных подпространств L₁ и L₂ , где L₁= <е₁,…,е_m>, L₂= <е_m+1,…, е_n>.

Вывод: Lⁿ распадается в прямую сумму j- инвариантных

подпространств Û [ ] в некотором базисе е имеет блочно- диагональный вид (16.2).

Date: 2015-09-25; view: 400; Нарушение авторских прав