
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Линейных операторов
|
|
Мы установили, что упростить вид матрицы л.о. j: L® L можно, если у этого оператора существует хотя бы одно инвариантное подпространство в L. Еще лучше с упрощением матрицы дело обстоит тогда, когда в L существует два j- инвариантных подпространства и сумма их – прямая. Вообще, чем больше в L имеется j- инвариантных подпространств, сумма которых – прямая, тем сильнее можно упростить матрицу л.о. j. Самая лучшая ситуация с упрощением матрицы имеется тогда, когда L равно прямой сумме п одномерных j- инвариантных подпространств.
Рассмотрим вопрос, как находить одномерные j- инвари-
антные подпространства. Пусть V – одномерное подпростра-
нство, V = <s >, s ¹ 0 Þ V= {a s | a Î P }. Очевидно, V –
j- инвариантное подпространство Û j VÌ V Û j sÎ VÛ
$lÎ P такой, что j s =l s.
Определение. Пусть L – линейное пространство над полем Р, j: L® L – линейный оператор. Вектор sÎ L называется собственным вектором л.о. j, если s ¹ 0 и $lÎ Р такое, что j s = ls. l называется собственным значением (собственным числом) оператора j.
По определению 0L не является собственным вектором, хотя j 0L = 0L = l0L " lÎ Р.
Пример. Для L = С∞(-¥, +¥) - линейного пространства бесконечно дифференцируемых функций на числовой прямой, и л.о. j = d/dx: С∞(-¥, +¥) → С∞(-¥, +¥) вектор еkx является собственным вектором с собственным значением k.
Очевидно, что нахождение собственных векторов и нахождение одномерных j- инвариантных подпространств – эквивалентные задачи.
Рассмотрим, как находить собственные векторы. Пусть
j: Ln ® Ln - линейный оператор, е = {е1,…, еn } - базис в Ln.
Тогда х – собственный вектор для j Û $l Î Р такое, что j х=l х, и х¹ 0 Û (l×id - j)х= 0, и х¹ 0 Û хÎ Ker(l×id - j), и х ¹ 0. Таким образом, все ненулевые векторы из
Ker(l×id - j) являются собственными векторами оператора j, соответствующими собственному значению l. Но в силу теоремы 6 из п.15 Ker(l×id - j) ¹ {0} Û det(l×id - j) = 0 Û
det [ l×id - j ] = det(lE - [  ] ) = 0.
] ) = 0.
Рассмотрим cj(t)= det [ t×id -j ] = det(tE - [  ] ) - многочлен от t степени n c коэффициентами в Р. Очевидно,
] ) - многочлен от t степени n c коэффициентами в Р. Очевидно,
(l×id - j)х = 0Û (lE – [ j ] )× [ x ] = [ 0 ], причем ненулевые решения этой однородной системы линейных уравнений существуют Û l - корень многочлена cj(t).
Заметим, что в силу леммы из п. 14.2. det(t×id - j) не зависит от базиса e.
Определение. Многочлен c (t)= cj(t) называется характеристическим многочленом оператора j или матрицы [ j ], а уравнение c(t) = 0 называется характеристическим уравнением.
Таким образом, для нахождения собственных векторов линейного оператора j надо:
1. Найти корни l1,…, lk характеристического многочлена c (t) линейного оператора j, лежащие в Р.
2. Для каждого li , i = 1,…,k, решить однородную систему линейных уравнений (liE - [ j ] )× [ x ] = [ 0 ]. Её фундаментальная система решений даст множество линейно независимых собственных векторов с собственным значением li .
Замечание. Если Р – алгебраически замкнутое поле, то характеристический многочлен обязательно имеет некоторый корень l в Р, и, следовательно, для l существует собственный вектор, то есть любой корень является собственным значением оператора j. И значит, "j $ собственный вектор.
Если Р – не алгебраически замкнутое поле, то c (t) может не иметь корней в Р, и тогда, соответственно, в L не будет собственных векторов для оператора j.
Теорема. Характеристические многочлены эквивалентных матриц совпадают.
Доказательство. Пусть А~В Þ $ Т: А = Т -1ВТ Þ
cA(t)= |tE – A| = |tE - Т-1ВТ|=|Т-1(tE – В)Т|=|Т-1|×|(tE – В)|×|Т|= = |(tE – В)|= cB(t).
ÿ
Легко видеть, что
cA(t)= |tE – A| = 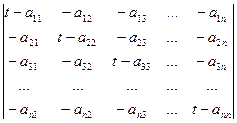 =
=
= (t – a11)×(t – a22)×… × (t – ann)+ слагаемые степени £ (n-2) =
= tn - (a11+ a22+…+ ann) tn-1 + …+ (-1)ndetA.
Определение. Для квадратной матрицы А =(аij) порядка n следом матрицы называется tr A = а11+а22+…+ аnn.
По теореме, если А~ В, то trA=trВ, так как cA(t)= cВ(t), а trA – второй коэффициент характеристического многочлена. Очевидно, что и все остальные коэффициенты характеристических многочленов для эквивалентных матриц совпадают, в том числе и последние, но это мы уже знаем. Отсюда, в частности, следует, что если trA ¹ trВ, то А и В не эквивалентны.
Лекция 28.
16.5. Теорема Гамильтона – Кэли. Любая квадратная матрица А является корнем своего характеристического многочлена: cA(А)=0.
Доказательство. Пусть п – порядок матрицы А, и В=(bij) – присоединенная матрица матрицы tE – A: B = (tE – A)* (см. 9.4). Тогда bij – алгебраические дополнения к элементам матрицы tE– A, то есть миноры (с точностью до знака) (п-1) -го порядка матрицы tE– A. Значит, bij – многочлены от t степени
£ п-1. Поэтому bij имеют вид bij = b(0)ij+ b(1)ijt + …+ b(п-1)ijtп-1, где все b(k)ij Î Р. Определим матрицы В(k) с элементами из Р: В(k) = (b(k)ij), k = 0, 1,…,п - 1. Тогда В = В(0)+ tВ(1))+…+ tп-1В(п-1). По свойству присоединенной матрицы
В×(tE – A) = |tE – A|×Е. (16.3)
Пусть cA(t)= |tE – A|= с0 + с1t+…+ сп-1 tп-1+ tп. Из формулы
(16.3) получаем:
(В(0)+ tВ(1) +…+ tп-1В(п-1))(tE– A) = (с0 + с1t+…+ сп-1 tп-1+ tп)×Е. Сравним коэффициенты при одинаковых степенях t и запишем результат в таблицу:
| При t0: | -В(0)А | = с0Е | ×А0 =Е |
| При t1: | -В(1)А+ В(0) | = с1Е | ×А |
| При t2: | -В(2)А+ В(1) | = с2Е | ×А2 |
| ....... | .......... | ...... | ..... |
| При tп-1: | -В(п-1)А+ В(п-2) | = сп-1Е | ×Ап-1 |
| При tп: | В(п-1) | = спЕ | ×Ап |
Затем домножим все наши равенства на степени матрицы А, стоящие справа, и сложим их. Получим:
0 = с0Е+ с1А+…+ сп-1 Ап-1+ Ап =cA(А)×
ÿ
Следствие. [ cj(j) ] = c [ j ] ( [ j ] )= 0 Þ cj(j)= 0.
Date: 2015-09-25; view: 395; Нарушение авторских прав