Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
При изменении базисов
|
|
Пусть e ={e1, …,en} и e¢ = {e¢1, …,e¢n} – два базиса в пространстве Ln, u ={u1, …,um} и u¢ = {u¢1, …,u¢m} – два базиса в пространстве Lm, Т1 =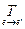 
, Т2 = 
- матрицы перехода, и j: Ln ® Lm - линейное отображение. Найдем зависимость между матрицами [ 
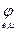] = [ j ] и [ 
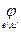] = [ j ] ¢ линейного отображения j в базисах е, и и е¢, и¢ соответственно.
Если y = j х, то в базисах е, и имеем [ y ] = [ j ][ x ], а в базисах е¢, и¢ соответственно [ y ] ¢ = [ j ] ¢ [ x ] ¢. Но [ x ] = Т1 [ x ] ¢,
[ y ] =Т2 [ y ]¢, так что Т2 [ y ]¢ = [ j ] Т1 [ x ]¢ и [ y ]¢ =Т2-1 [ j ] Т1 [ x ]¢ = [ j ]¢[ x ]¢. Отсюда [ j ] ¢ = Т2-1 [ j ] Т1 или [ 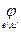] = -1 [ 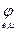] 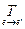. В частном случае при Ln = Lm, е = и, е ¢ = и ¢ для линейного оператора
j: Ln® Lп получаем [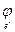 
] = 
[ 
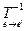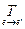] , то есть [ j ] ¢= Т-1 [ j ] Т,
где [ j ] = [ ], [ j ] ¢= [ 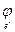], Т = .
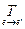Лемма. Для линейного оператора j: Ln ® Lп det [ ] не
зависит от базиса.
Доказательство. det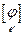 
= det [ j ] ¢ = det Т-1det [ j ] det Т=
= det (Т-1Т)det [ j ] = det Е det [ j ] = det [ j ] = det [ ].
Определение. Определителем detj линейного оператора
j: Ln ® Lп называется det [ ] - определитель матрицы линейного оператора j в произвольном базисе е.
Из леммы следует, что наше определение корректно.
Date: 2015-09-25; view: 299; Нарушение авторских прав