Операторы

Определение. Линейный оператор j: Lⁿ ® Lⁿ называется

диагонализируемым, если существует базис е в Lⁿ такой, что [ ] - диагональная матрица, [ ] = diag(l₁,…,l_п).

Теорема 1 (необходимое и достаточное условие диагонализируемости). Линейный оператор j: Lⁿ ® Lⁿ имеет в некотором базисе е диагональную матрицу [ ] = diag(l₁,…,l_п) Û базис е состоит из собственных векторов л.о. j, а l₁,…,l_п – собственные значения оператора j.

Доказательство.

Þ. Пусть в базисе е = {е₁,…, е_n } матрица [ ] = diag(l₁,…,l_п). Тогда "i=1,…,п j е_i= l_i× е_i Þ базис е состоит из собственных векторов л.о. j, с собственными значениями l₁,…,l_п .

Ü. Если базис е = {е₁,…, е_n } состоит из собственных векторов л.о. j, с собственными значениями l₁,…,l_п , то "i=1,…,п j е_i= l_i× е_i Þ [ ] = diag(l₁,…,l_п).

ÿ

Рассмотрим, при каких условиях в Lⁿ существует базис из собственных векторов л.о. j.

Лемма. Собственные векторы л.о. j, соответствующие различным собственным значениям, линейно независимы.

Доказательство. Пусть s₁,…, s_k – собственные векторы л.о. j с различными собственными значениями l₁,…,l_k. Проведем доказательство индукцией по k.

При k = 1 вектор s₁ линейно независим, так как s₁ ¹ 0.

Пусть для k - 1 утверждение верно, то есть s₁,…, s_k-1 линейно независимы. Покажем, что тогда s₁,…, s_k-1, s_k линейно независимы. Предположим, что

a₁s₁+…+a _k-1s_k-1+a _k s_k = 0. (17.1)

Применим к левой и правой частям этого равенства л.о. j. Получим:

a₁l₁s₁+…+a _k-1l _k-1s_k-1+a _kl_ks_k = 0. (17.2)

Теперь умножим равенство (17.1) на l_k и вычтем его из (17.2). Получим a₁(l₁ -l_k)s₁+…+a _k-1(l _k-1 -l_k)s_k-1= 0. Но s₁,…, s_k-1 линейно независимы Þ a₁(l₁ -l_k)=…=a _k-1(l _k-1 -l_k)= 0 Þ a₁=…=a _k-1=0, так как l₁ -l_k ¹ 0,…, l _k-1 -l_k ¹ 0. Теперь из (17.1) получаем, что a _k s_k = 0Þ a _k= 0 (так как s_k ¹ 0) Þ s₁,…,s_k - линейно независимы.

ÿ

Пример. В линейном пространстве L = С^∞(-¥, +¥) бесконечно дифференцируемых функций на числовой прямой для л.о. j = d/dx: С^∞(-¥, +¥) → С^∞ (-¥, +¥) (см. пример из п.16.4) векторы е^аx являются собственными векторами, и поэтому любая система векторов { е^аx,е^bx,…,е^сx} с различными а, b,…,с – линейно независима.

Теорема 2 (достаточное условие диагонализируемости).

Если характеристический многочлен c_j(t) линейного оператора j: Lⁿ ® Lⁿ имеет п различных корней в поле Р, то в Lⁿ существует базис из собственных векторов (в котором матрица [ j ] – диагональна).

Доказательство. Действительно, в этом случае по лемме в Lⁿ существуют п линейно независимых собственных векторов л.о. j, которые образуют базис из собственных векторов (в котором по теореме 1 матрица [ j ] – диагональна).

ÿ

Замечание. Условие в теореме 2 достаточное, но не необходимое: л.о. id: Lⁿ ® Lⁿ имеет единственное собственное значение l₁ =1, но любой базис пространства Lⁿ состоит из собственных векторов л.о. id.

Рассмотрим, почему л.о. j: Lⁿ ® Lⁿ может не быть диагонализируемым. Во-первых, это может быть из-за того, что поле Р не алгебраически замкнуто, и характеристический многочлен c_j(t) имеет в Р меньше, чем п корней. Например, для поворота плоскости на угол p/2 характеристический

многочлен t²+1 не имеет действительных корней, и, очевидно, собственных векторов для этого поворота также нет. Во-вторых, для некоторого собственного значения l₀ Î Р кратности k >1 число соответствующих линейно независимых собственных векторов может быть меньше, чем k (см. теорему 3). Например, для л.о. j с матрицей [ j ] = 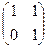в базисе е = {е₁,е₂ }, очевидно, l_1,2 =1 - собственное значение кратности 2, но существует лишь один соответствующий линейно независимый собственный вектор – это е₁.

Теорема 3. Пусть Lⁿ – линейное пространство над полем Р, j: Lⁿ ® Lⁿ - линейный оператор, l₀ – корень характеристического многочлена c_j(t) кратности k ³ 1. Тогда число линейно независимых собственных векторов оператора j с собственным значением l₀ не превосходит k.

Доказательство. Пусть dim Ker(l₀ id - j)= m, {s₁,…,s_m} – базис подпространства Ker(l₀ id - j) (m – это и есть максимальное число линейно независимых собственных векторов оператора j с собственным значением l₀ ). Дополним систему векторов {s₁,…, s_m} до базиса е всего пространства Lⁿ:

е = {s₁,…, s_m, а_m+1,…, а_п}. Тогда [ ] = = ,

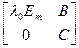где Е_m – единичная (m´ m)- матрица, 0 – нулевая (n – m)´ m -матрица, В – некоторая m´(n – m) -матрица, С - некоторая

(n – m)´ (n – m) -матрица. Характеристический многочлен

c_j(t)= det(tЕ - [ ] )=det 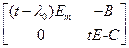=(t -l₀)^m×g(t), где g(t) – некоторый многочлен от t. Поэтому k ³ m, то есть максимальное число линейно независимых собственных векторов оператора j с собственным значением l₀ не превосходит кратности корня l₀ в характеристическом многочлене.

ÿ

Лекция 29.

Date: 2015-09-25; view: 371; Нарушение авторских прав