Алгебры матриц

Пусть L= Lⁿ - линейное пространство над полем P, Ф(Lⁿ) – множество линейных операторов j: Lⁿ ® Lⁿ. Тогда из пп.13.2-13.4 следует, что < Ф(Lⁿ),+, 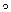, 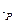> - некоторая универсальная алгебра.

Теорема. < Ф(Lⁿ),+, 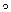, 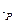> - алгебра.

Один из возможных способов доказательства этой тео­ремы состоит в доказательстве следующих трех утвержде­ний:

1. Множество Ф(Lⁿ,L^m)={j: Lⁿ ® L^m} линейных отображе­ний из Lⁿ в L^m с операциями сложения и умножения на эле­менты поля является линейным пространством над полем P.

2. Ф(Lⁿ) – ассоциативное унитарное кольцо относительно операций сложения и умножения (композиции) линейных операторов.

3. Ф(Lⁿ) – алгебра относительно операций из пп.1,2.

Мы докажем эту теорему иначе.

Определение. Пусть A =<A, W_A >, B =<B, W_B > - универсальные алгебры с носителями A, B и множествами операций W_A, W_B соответственно. Отображение c: A ® B называется изоморфизмом универсальных алгебр, если:

1. c: A® B – биекция носителей,

2. $ биекция c_W: W_A ® W_B такая, что для любой n- арной операции wÎW_A операция c_W (w)=w¢ÎW_B также n- арная, и

" a₁,…,a_nÎ А выполняется c(a₁…a_nw)=c(a₁)…c(a_n)w¢.

Date: 2015-09-25; view: 318; Нарушение авторских прав