Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Доказательство. Þ . Если Kerj ' х ¹ 0, то j х = j 0 = 0Þ j - не инъекция
Þ. Если Kerj ' х ¹ 0, то j х = j 0 = 0Þ j - не инъекция.
Ü. Если j х1= j х2, то j х1 - j х2= j (х1 – х2)= 0 Þ
х1 – х2Î Kerj = {0} Þ х1 – х2= 0 Þ х1 = х2 Þj - инъекция.
ÿ
Замечание. Kerj - мера неинъективности отображения
j: если y =j х, то j -1y = х + Kerj.
Доказательство.
1. j (х + Kerj)= j х +j(Kerj)=у + 0 = у Þ j -1y Ê х + Kerj.
2. Если х¢Î j -1y, то j х¢ = j х = у Þ j(х¢ - х) = 0
Þ х¢ - х Î Kerj Þ х¢ Î х + Kerj Þ j -1y Í х + Kerj.
ÿ
Теорема 4 (структура Imj). Пусть j: L ® L¢ - линейное
отображение, е = {е1,…, еn} – базис в L, е¢ = {е¢1,…, е¢m} – базис в L¢, [ j ] - матрица j в базисах е, е¢. Тогда:
1. Imj = <j е1,…,j еn>,
2. dim Imj = rg [ j ].
Доказательство.
1. "xÎL, x=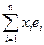 
, j х = j()= 
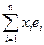Î<j е1,…,j еn>
Þ Imj = <j е1,…,j еn>, {jе1,…,j еn} – система образующих для Imj.
2. dim Imj - это ранг системы векторов {j е1,…,j еn}, то есть ранг системы столбцов координат этих векторов [ 
] ,…, [ 
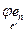], которые являются столбцами матрицы [ j ]. Отсюда dim Imj = rg [ j ].
ÿ
Следствие. Так как в равенстве dim Imj = rg [ j ] левая
часть от базиса не зависит, то и rg [ j ] во всех базисах один и
тот же.
Определение. Пусть j: Ln® Lm - линейное отображение. Рангом отображения j называется число dim Imj = rg [ j ], которое мы будем обозначать rgj.
Дефектом отображения j называется число dim Kerj, которое мы будем обозначать defj.
Теорема 5. rgj + defj = n = dimLn.
Доказательство. Выберем базис {е1,…,еd} в подпространстве Kerj и дополним его до базиса {е1,…, еd, еd+1,…, еn} всего пространства Ln. Тогда Imj =<j е1,…,j еd, j еd+1,…,j еn>=
= <j еd+1,…,j еn>, так как j е1=…=j еd= 0. Покажем, что {j еd+1,…,j еn} – базис в пространстве Imj. Для этого достаточно доказать, что векторы {j еd+1,…,j еn} – линейно независимы. Пусть ad+1j еd+1 +…+ anj еn = 0 Þ
j(ad+1еd+1+…+anеn) = 0Þ
ad+1 еd+1 +…+ an еn Î Kerj = <е1,…, еd> Þ
ad+1еd+1 +…+ anеn=a1е1+…+ad еd Þ
a1е1+…+ad еd - ad+1 еd+1 -…-anеn= 0. Но {е1,…,еn} линейно независимы. Значит, все a i= 0. Таким образом, {jеd+1,…,j еn} – базис в пространстве Imj, dim Imj = n – d = n – dim Kerj Þ
rgj + defj = n = dimLn.
ÿ
Следствие. Ln=<е1,…, еd, еd+1,…, еn>=<е1,…, еd> Å
Å <еd+1,…, еn>=Kerj Å <еd+1,…, еn>, и j: <еd+1,…, еn>® Imj - изоморфизм линейных пространств.
Лекция 27.
Теорема 6. Для линейного оператора j:Ln ® Ln эквивалентны следующие 10 условий:
1. Kerj = {0},
2. defj = 0,
3. rgj = n,
4. Imj = Ln,
5. j - инъекция,
6. j - сюръекция,
7. j - биекция,
8. $ j -1,
9. $ [ j ] -1,
10. detj ¹ 0.
Доказательство.
Очевидно, 1Û2 и 3Û4Û6 из определения, 2Û3 из тео-
ремы 5, 1Û5 из теоремы 3, 5&6Û7 из определения. Так как rgj = rg [ j ], а detj = det [ j ], то из теории определителей 3Û10, а из теории матриц 10Û9. Эквивалентность 9Û8 следует из того, что [ j ] -1= [ j -1 ]. Либо можно доказать эквивалентность 7Û8 следующим образом: 8Þ7 – из определения, а если имеет место 7, то, очевидно, отображение j -1$, и нам требуется лишь доказать его линейность. Пусть j -1х = u,
j -1y = v Þ j u = х, j v = y Þ j(a u+b v) =a х +b yÞ
j -1(a х +b y) = a u+b v = aj -1х + bj -1y Þ j -1 – линейно.
ÿ
Определение. Линейный оператор j называется невырожденным, если выполняется любое из десяти эквивалентных условий из Теоремы 6. В противном случае оператор называется вырожденным.
ИНВАРИАНТНЫЕ ПОДПРОСТРАНСТВА
Определение. Для линейного оператора j:L ® L подпространство V Í L называется инвариантным относительно j (или j -инвариантным), если jV Í V ("хÎV j хÎV).
Date: 2015-09-25; view: 354; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |