Ранговые коэффициенты связи

Ранговыми коэффициентами связи называются меры связи, позволяющие вычислять степень согласованности в ранжировании одних и тех же объектов по двум различным основаниям или по двум различным признакам. Мы неоднократно ссылались на необ­ходимость для социолога такого рода коэффициентов. Например, при построении шкалы суммарных оценок появлялась необходи­мость в проверке согласованности результатов, полученных по ито­говой шкале, с данными по исходным шкалам (суждениям).

Коэффициентов ранговой корреляции много. Для того чтобы понять их схожесть и различие, необходимо вначале несколько отой­ти от таблиц сопряженности и нашей задачи. А вам придется вер­нуться к разделу книги, посвященному процедуре ранжирования. Как было отмечено, такая процедура возникает у социолога как на этапе измерения, так и на этапе анализа данных. В любом случае возникает задача определения степени согласованности двух ран­жированных рядов. Представим себе, что для одной и той же сово­купности объектов получили два ранжированных ряда. Например, по тем же будущим профессиям студента. Значит, объектов у нас всего шесть по числу профессий. Пусть первый ряд получен по степени уменьшения индекса удовлетворенности учебой. Второй ряд ¾ по степени уменьшения индекса уверенности в трудоустрой­стве по профессии после окончания вуза. Далее будем коротко на­зывать эти признаки — «удовлетворенность» и «уверенность».

В данном контексте мы не будем обсуждать вопрос, каким об­разом измерены эти признаки как характеристики группы. Заметим лишь, что они могли быть получены с помощью шкалы суммарных оценок или как групповые индексы, примеры которых были приве­дены в «Лекциях».

В случае полной (максимальной) согласованности ранжирова­ния по этим двум признакам естественно предположить наличие тесной (сильной) связи между признаками «удовлетворенность» и «уверенность». Такая связь может быть и прямой (чем больше удов­летворенность, тем больше уверенность), и обратной (чем больше удовлетворенность, тем меньше уверенность). Из этого проистека­ет, что логично изменяться значениям коэффициента ранговой кор­реляции от -1 до +1. Этим свойством обладают все приведенные ниже коэффициенты.

Приведем примеры нескольких коэффициентов, а затем пояс­ним их содержательный смысл.

Мера g (гамма) Л. Гудмена и Е. Краскала (L. Goodman, E.Kraskal)

Первая из этих мер в работе [8, с. 135], обозначена как «g Гудмана». Эти меры удачно описаны в работе [1, с. 37—40]. Вы, конечно, обратили внимание, что у всех приведенных мер один и тот же числитель, а знаменатели различны. Прежде всего рассмот­рим числитель, ибо он несет в себе основное содержание коэффи­циентов, В таблице 3.5.4 представлены два ранжированных ряда. Объекты ранжирования ¾ будущие профессии. Они приведены в таблице для удобства в том порядке, в котором их ранги во втором ряду возрастают, т. е. в порядке убывания степени уверенности. Число рангов равно числу объектов, связанных рангов (одинако­вых) в наших рядах не наблюдается.

Таблица 3.5.4

Примеры двух ранжированных рядов

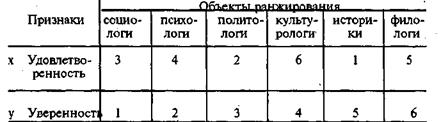
Из этой таблицы видим, что политологи в первом ряду имеют ранг 2, а во втором ¾ ранг 3, а историки в первом ряду ¾ ранг 1, во втором ¾ ранг 5. Для того чтобы оценить степень согласованности наших, грубо говоря, «ранжировок», можно применить тот же прием, который был применен при вычислении меры качественной ва­риации. Образуем из наших шести объектов различные пары. Таких пар будет 6x5/2=15. Возьмем отдельную пару объектов. Ранги, соот­ветствующие первому объекту, обозначим (i₁, j₁), а второму ¾ (i₂, j₂). Эти ранги могут находиться в различных отношениях. Возмож­на одна из двух ситуаций, каждая из которых включает два возможных соотношения между рангами (1а, 16, 2а, 26).

В первой ситуации ранги как бы согласованы, а во втором не согласованы. Подсчитаем, для скольких пар из 15-ти наблюдается согласованность, и обозначим число таких пар через S. Затем под­считаем, для скольких пар наблюдается несогласованность, и обо­значим число таких пар через D. В числителе всех приведенных выше мер стоит как раз разница между числом согласованных и несогласованных пар объектов. Для примера наших ранжирован­ных рядов величина (S-D) равна:

S-D = (3-2) + (2-2) + (2-1) + (0-2) + (1-0) = 1.

Здесь первая скобка ¾ результат анализа согласованности / несогласованности рангов в парах, образованных первым объектом с остальными пятью, т. е. в парах (1 и 2), (1 и З), (1 и 4), (1 и 5), (1 и 6). Среди них согласованность (случай 1а) — в трех парах, а несогласо­ванность (случай 26) — в двух парах. Вторая скобка ¾ результат ана­лиза пар, образованных вторым объектом, т. е. пар (2 и 3), (2 и 4), (2 и 5), (2 и 6). Среди них в двух парах согласованность, а в двух ¾ не­согласованность. Последняя скобка ¾ результат анализа пары (5 и 6).

Мы рассматривали случай отсутствия связанных рангов, поэто­му для определения степени согласованности можно использовать первый из трех коэффициентов, приведенных выше. Знаменатель для его вычисления равен:

S+D = (3+2) + (2+2) + (2+1) + (0+2) + (1+0) = 15

или просто числу различных возможных пар, т. е. 6x5/2=15

Тогда g» 0,07. В самом деле степень согласованности в наших ранжированных рядах очень мала. Второй из трех коэффициентов учитывает наличие связанных рангов. Кроме соотношений (1а; 1б;

Число пар, соответствующих третьей ситуации (есть связанные ранги во втором ряду), обозначим через Т_у. Число пар, соответ­ствующих четвертой ситуации (есть связанные ранга в первом ряду), обозначим через Т_х. Второй коэффициент учитывает число связан­ных рангов в том и другом ранжированных рядах.

И наконец, обратите внимание на коэффициент d_y/x. Мер Сомерса всего три по аналогии с мерами «лямбда» Гуттмана и «гамма» Гудмена и Краскала, т. е. ранговые коэффициенты связи бывают и на­правленные. Мы привели только одну из трех мер Сомерса. В случае ее использования вопрос о степени согласованности в ранжированных рядах звучит несколько иначе, а именно: влияет ли «уверенность» на «удовлетворенность» и, наоборот, влияет ли ранжирование по «удов­летворенности» на ранжирование по «уверенности». Разумеется, только в смысле того, что ранжирование объектов по степени убывания «удов­летворенности» (признак У) зависит от ранжирования по степени убы­вания «уверенности» (признак X). Поэтому в знаменателе учитыва­ются связанные ранги только для признака У.

А теперь представим себе, что речь идет об анализе связи по таблице сопряженности (корреляционная таблица) двух признаков, имеющих порядковый уровень измерения. Допустим, что у каждо­го нашего студента-гуманитария есть оценка не только удовлетво­ренности учебой, но и удовлетворенности собой. Оба признака имеют порядковый уровень измерения. Для изучения связи между ними используются те же ранговые меры связи. Их значения рассчитыва­ются по тем же формулам, ибо можно всех наших студентов (объекты ранжирования) упорядочить и получить два ранжированных ряда. Первый ¾ по степени убывания (возрастания) удовлетворенности учебой, а второй ¾ по убыванию (возрастанию) удовлетворенности собой. Естественно, у нас будут сплошь связанные ранги. Напом­ним, что число рангов равно числу объектов, т. е. 1000. Реально никто такое ранжирование не проводит, а просто вычисляются по таблице сопряженности число согласованных пар, число несогла­сованных и число связанных рангов. Существуют коэффициенты ранговой корреляции для быстрого счета (коэффициент Спирмена), но в век компьютеров они уже утратили свою актуальность.

Мы рассмотрели все коэффициенты, необходимые для первоначального понимания того, что они из себя представляют, и почему их так много. В завершение этого раздела книги несколько слов о том, что все эти коэффициенты являются статистиками, т.е. для них можно построить доверительный интервал. Тот интервал, в котором находится истинное значение коэффициента, т. е. для изучаемой генеральной совокупности. Доверительные интервалы есть для «лямбда» [1, с. 34], «may» [1, с. 36], для коэффициентов ранго­вой корреляции [9, с. 185—187].

В рамках книги не ставилась цель привести все меры или дать их классификацию, ибо для этого необходимы серьезные знания в области науки под названием теория вероятности и математическая статистика. Более того, мы намеренно не рассматривали меры для изучения связи между признаками, измеренными по «метрическим» шкалам (по всем, по которым уровень измерения выше порядкового). Такая позиция обусловлена сочетанием двух факторов процесса обучения студентов. Во-первых, в эмпирической социологии такого рода шкалы встречаются реже других. Во-вторых, в читаемом сту­дентам курсе «Теория вероятности и математическая статистика» понятие «связь» вводится именно с такого рода мер связи.

Date: 2015-09-24; view: 385; Нарушение авторских прав