О значимости значений коэффициентов

Каждый закон распределения имеет параметры. Примером за­кона является уравнение прямой у — аХ + b. Это семейство пря­мых. Здесь параметрами являются а, b. Аналогично можно рассуж­дать во всех случаях законов, известных вам из школьной программы (парабола, гипербола, синусоида и т. д.). Только теперь вы имеете дело с более сложными законами: нормальным, хи-квадрат и т. д. Более того, для некоторых законов, например для хи-квадрат, даже нельзя в явной форме записать формулу.

Некоторые законы табулированы, т. е. существуют математи­ческие таблицы (они есть во многих книгах, где описываются мето­ды математической статистики), из которых можно определить таб­личное значение некоторой статистики при заданных параметрах распределения. Например, табличное значение для величины «хи-квадрат» ¾ это то значение, которое оно принимает при статисти­ческой независимости.

Кроме параметров для обращения к математическим таблицам необходимо обязательно задать так называемый уровень значимости (а), т.е. уровень возможной ошибки. В математической статис­тике на основе данных выборки ни один вывод не делается без некоторой ошибки. Значение а может быть равным 0,10; 0,05; 0,01. Тогда наши выводы будут верны в 90 случаях из ста, если социолог задал первое из этих значений. Для второго уровня значимости вы­воды верны в 95 случаях из ста, а для третьего ¾ в 99 случаях из ста, а для четвертого 999 случаев из тысячи.

Таким образом, если некоторая величина табулирована, то, за­давшись уровнем значимости и параметрами закона распределения, можно узнать ее теоретическое значение. А у нас всегда есть реаль­ное значение. Сравнение этих значений и позволяет проверять ста­тистические гипотезы.

Возвращаясь к коэффициенту Юла и статистики «хи-квадрат», следует сказать, что первый из них имеет нормальный закон распределения, а второй ¾ распределение хи -квадрат. Параметром для нормального закона является дисперсия, а параметром для хи-квад-рат ¾ число степеней свободы, равное (r-l)(s-l). По существу, число степеней свободы ¾ число ячеек в таблице сопряженности, которые могут изменяться свободно (отсюда и название число «степеней сво­боды») при заданных маргинальных частотах. В нашем случае реальное значение «хи -квадрат» равно c² = 125,6, а табличное значение = 10,85 при уровне значимости, равной 0,05, и числе степеней свободы (r-l)(s-l)=20. Таким образом, 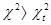, т. е. отклонение от нуля значимо. Признаки «будущая профессия студента» и «удовлетворенность учебой» статистически зависимы.

Понятие значимости тесно связано с понятием «доверитель­ный интервал». Для каждой статистики это интервал, в котором содержится «истинное» (для генеральной совокупности) значение этой статистики. Если истинное значение коэффициента Юла обо­значить через Q^t, а реально вычисленное через Q, то доверитель­ный интервал выглядит:

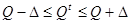
Для каждой статистики величина D определяется в зависимос­ти от закона распределения статистики и, естественно, в помощью математических таблиц, где эти законы табулированы. Приводить формулы для вычисления доверительных интервалов мы не будем. К примеру, социолога всегда интересует значимость процентов. В работе [8, с. 191—195] вы можете найти формулу для вычисления доверительного интервала в этом случае.

Из такого упрощенного анализа значимости и законов распределе­ния социологу необходимо усвоить, что умные люди, работающие в далекой от него науке под названием математическая статистика, владеют большим аппаратом для решения социологических задач. Это не означает, что вы должны эту науку изучить досконально, но это означает, что Вы должны научиться задавать таким людям правиль­но поставленные вопросы, и не ожидать от математики того, чего она не может дать.