И четвертой степени удовлетворенности

Одним из языков анализа связи между этими свойствами явля­ется поиск ответа на вопрос: наблюдается ли статистическая зави­симость между этими свойствами. Если наблюдается статистичес­кая независимость У (удовлетворенные учебой на «четыре») от П (политологи), то 30/250 (доля удовлетворенных учебой политологов среди всех удовлетворенных учебой на четыре балла) должно рав­няться 70/750 (доля «остальных» политологов среди всех «осталь­ных»). То же самое запишем в общем виде:

Из этого следует, что a(d + b) = (а + c)d —> ab = cd. Тогда разность ab —cd можно использовать как меру отклонения от стати­стической независимости. Такое же соотношение получим, если будем рассуждать по-другому. Если статистическая независимость П от У наблюдается, то, 30/100 (доля удовлетворенных политологов среди политологов) должно равняться 220/900 (доля удовлетворен­ных «не политологов» среди всех «не политологов»).

На этой разности и основан коэффициент Юла (G, Yule), кото­рый имеет следующий вид:

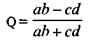
Знаменатель введен для того, чтобы значения этого коэффици­ента изменялись от -1 до +1. Если вы видите коэффициенты двух­этажные (со знаменателями), то очень часто (но не всегда) наличие знаменателя служит как бы для нормирования интервала измене­ния значений коэффициента. Содержательный смысл меры связи, как правило, передает числитель. Рассмотрим свойства (поведение) этого коэффициента:

1. Он равен единице либо когда с = 0 /схема 3.4.1 а)/, либо d = 0 /схема 3.4.1 б)/. В первом случае все «не политологи» относятся к «остальным» по удовлетворенности. Обратное утверждение не­верно. Во втором случае все политологи удовлетворены учебой на 4 балла. Опять же обратное утверждение будет неверным.

2. Он равен минус единице, если а = 0 /схема 3.4.1 в)/ или b = 0 /схема 3.4.1 г)/. В первом случае все политологи относятся к «остальным» по удовлетворенности. Во втором случае все «не политологи» удовлетворены учебой на четыре балла. Обратные ут­верждения неверны.

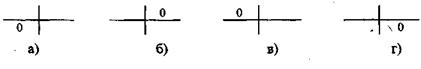
Схема 3.4.1

3. Коэффициент равен нулю, если ab = cd, т. е. в случае стати­стической независимости наших изучаемых свойств.

В нашем случае коэффициент равен 0,14. Естественным обра­зом, возникает вопрос, каким будет значение коэффициента для генеральной совокупности. Ведь пока мы получили только оценку связи по выборочной совокупности. Значение коэффициента не­большое, но отличное от нуля, поэтому возникает другой вопрос. Значимо ли это отличие от нуля или мы получили ненулевое значе­ние случайно? Если это отклонение незначимо, то наблюдается ста­тистическая независимость наших свойств (быть политологом и быть удовлетворенным учебой на четыре балла). И наоборот, если это отклонение значимо, то имеем случай статистической зависимости. Для определения значимости и для определения «истинного» зна­чения (для генеральной совокупности) необходим аппарат матема­тической статистики, а именно аппарат проверки статистических гипотез. Ихне следует путать с содержательными гипотезами ис­следования. К этому вопросу мы вернемся несколько позже после введения так называемой статистики хи-квадрат.

Рассмотрим использование меры Юла в сравнительном кон­тексте. Пусть целевое свойство ¾ «быть удовлетворенным учебой на четыре балла». Попытаемся определить, какая из будущих про­фессий теснее связана с этим свойством, сильнее влияет на по­добную удовлетворенность. По данным, представленным в табли­це 3.3.1, сформируем таблицы сопряженности вида (2x2) для подсчета шести значений для шести будущих профессий. Так как для политологов значение коэффициента уже было получено по таблице 3.4.1, то ниже на схеме 3.4.2 приведены таблицы для оставшихся пяти будущих профессий. В этих таблицах приведены только абсолютные частоты. Целевой признак обозначен как (У). (+У) и означает обладать свойством «удовлетворенности учебой четыре балла», а (-У) ¾ не обладать, т. е. остальные варианты удовлетворенности учебой.

(2) (3) (4) (5) (6)

социологи культурологи филологи психологи историки

Схема 3.4.2. Таблицы сопряженности «удовлетворенность учебой на 4 балла» с будущими профессиями студентов

Для политологов коэффициент Юла был равен Q,=0,14. Для социологов Q₂=0,l6, так как

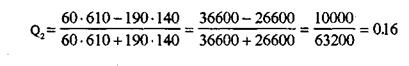
Аналогичным образом вычисляются значения коэффициента для Культурологов, филологов, психологов и историков. Соответствен­но получим следующие значения:

Q₃=0,40; Q₄ =-0,33; Q, =0,13; Q₆=-0,29.

Таким образом, если не учитывать, прямая (значения коэффи­циента положительные) или обратная (значения коэффициентов отрицательные) связь, наши шесть профессий по степени влияния на удовлетворенность упорядочиваются следующим образом:

|Q₃|>|Q₄|>|Q₆|>|Q₂|>|Q₁|>|Q₅|

Свойства «быть культурологом» и «быть филологом», скорее всего, связаны со свойством «удовлетворенность учебой на четыре балла» и влияют на него. Свойства «быть психологом» и «быть политологом», скорее всего, не влияют. От них удовлетворенность учебой не зависит. Еще раз хочется напомнить, в каком смысле «влияет», в каком смысле «зависит». Пока только в смысле статис­тической зависимости. Почему мы говорим «скорее всего»? Пото­му что по формальным критериям может оказаться, например, что все значения коэффициентов незначимо отличаются от нуля. Полученный результат ранжирования — лишь контекст для формиро­вания новых содержательных гипотез и усложнения моделей изуче­ния связи.

Date: 2015-09-24; view: 311; Нарушение авторских прав