Непосредственная ¾ опосредованная связь

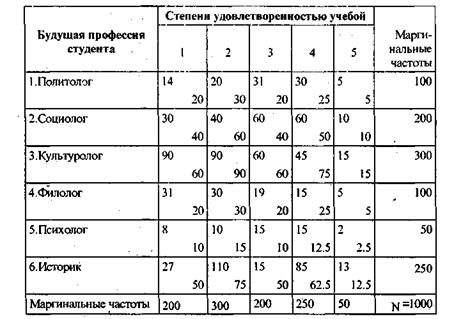
По таблице 3.4.1 коэффициент Юла показывает скорее на статистическую независимость, чем на статистическую зависимость, так как Q₁ = 0,14. Социологу может показаться сей статистический факт странным, так как не согласуется с его содержательными ги­потезами. Например, из предыдущих исследований могло быть из­вестно, что студенты-политологи в основном удовлетворены уче­бой. Сомнения социолога будут вполне оправданы, ибо отсутствие непосредственной корреляционной связи еще не говорит об отсутствии связи вообще. Связь между двумя свойствами может быть опосре­дована третьим свойством. Маленькое значение коэффициента мо­жет быть обусловлено тем, что характер связи между «быть полито­логом» и «быть удовлетворенным учебой» различен, например, для юношей и девушек. Таблица 3.4.2 ¾ таблица сопряженности между свойствами «быть политологом» и «иметь четвертую степень удовлетворенности учебой» для девушек, а таблица 3.4.3 соответственно для юношей. Проверьте: сумма частот в ячейках вида (i,j) в этих двух таблицах равна частоте, соответствующей аналогичной ячейке таблицы 3.4.1.

Таблица 3.4.2

Таблица сопряженности для девушек

Таблица 3.4.3

Таблица сопряженности для юношей

Подсчитаем коэффициент Юла для девушек (Q_f) и для юношей (Q_m). Первый будет равен примерно 0,9, а второй равен ¾ 0,7.

Во-первых, нетрудно заметить, что в том и другом случае ско­рее наблюдается статистическая зависимость, чем независимость. Во-вторых, в самом деле характер связи для наших подвыборок дей­ствительно различен. Для девушек получен следующий результат: либо почти все будущие политологи удовлетворены, либо не поли­тологи по удовлетворенности относятся к «остальным». Для юно­шей совершенно другой результат, а именно: либо почти все поли­тологи по удовлетворенности «остальные», либо «не политологи» удовлетворены учебой.

По этой причине значение коэффициента Юла, полученное без учета пола студента, и показало отсутствие связи. Такая ситуация для социолога может быть обозначена как ложное отсутствие кор­реляционной связи, проистекающее из существования опосредо­ванной связи, характер которой диаметрально противоположный на отдельных группах объектов. Этот пример показывает, что кон­кретные значения коэффициентов интерпретировать необходимо очень осторожно. Графически этот случай иллюстрирует граф, изоб­раженный на рис.3.4.2. Связь между признаками 1 и 6 не наблюда­ется. В то же время наблюдается связь между признаками 1 и 5, а также между признаками 5 и 6.

Другая ситуация ложных корреляционных связей является бо­лее очевидной. Это когда большое значение коэффициента обус­ловлено не сильной связью между свойствами, а тем, что существо­вание каждого из этих свойств обусловлено одной и той же причиной. Подозрение вызывает треугольник на том же рис. 3.4.2. Интерпре­тация больших и маленьких значений коэффициентов требует при анализе особого внимания. Этот вывод относится в равной мере ко всем коэффициентам, с которыми работает социолог. Переходим к рассмотрению коэффициентов для случая таблиц сопряженности вида (r*s). Вернемся к нашей таблице 3.3.1, где r = 6, a s = 5. Прежде всего следует отметить, что в соответствие каждой ячейке можно поставить как прямую детерминацию (от профессии к удовлетворенности) с интенсивностью (процент по строке) и ем­костью (процент по столбцу), так и обратную (от удовлетвореннос­ти к профессии). Дальнейший анализ таблицы проводится по сово­купности этих характеристик. Для выделения сильных локальных связей обычно задаются ограничения на значения интенсивности и емкости. По сути, речь идет о ранжировании всех локальных свя­зей. В этом случае не ставится вопрос о взаимосвязи феноме­нов «будущая профессия» и «удовлетворенность учебой», а ищутся как бы цепочки детерминации, что в дальнейшем может быть ис­пользовано для формирования гипотез о факторных синдромах и причинно-следственных отношениях. Напомним, что восходящая стратегия анализа и служит для формирования новых гипотез в ис­следовании.

Упомянутый выше «язык» анализа локальных связей ¾ язык детерминации ¾ достаточно легко переводится и на многомерный случай. Однако к работе [13] следует обращаться, имея определен­ный уровень математической подготовки.

Меры связи, основанные на c² (хи-квадрат)

Представим себе, как будет выглядеть наша таблица сопряжен­ности в ситуации статистической независимости между феномена­ми «будущая профессия» и «удовлетворенность учебой». Нетрудно вспомнить, что при статистической независимости, например, для частоты в ячейке (1,4) выполняется соотношение:

Если теперь записать это в общем виде, т. е. для любой ячейки (i j), то в случае статистической независимости будет верно соотно­шение:

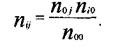
Эту частоту, для ее отличия от реальной, можно назвать теоре­тической и обозначить через 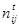.В таблице 3.4.4 приведены наши реальные частоты, взятые из таблицы 3.3.1, и теоретические. Пер­вые из них — в верхнем левом углу ячейки, а вторые — в нижнем правом углу ячейки.

Таблица 3.4.4

Таблица сопряженности: реальные и теоретические частоты

Является естественным для определения отклонения от стати­стической независимости воспользоваться разностью между ре­альными частотами и теоретическими (для случая статистической независимости), т.е. разностью вида 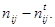Как и в случае введения формулы для вычисления дисперсии, нам нужны абсо­лютные значения этой разности, поэтому возводим ее в квадрат. Этот квадрат делим на теоретическую частоту, т. е. как бы норми­руем. Тем самым достигается независимость от объема ячейки. Все ячейки становятся равноправными независимо от их объема. Затем суммируем все эти отклонения по всем 30-ти ячейкам таб­лицы и получаем величину называемую хи-квадрат. Она выглядит следующим образом:

Для нашего примера эта величина вычисляется как сумма трид­цати членов:

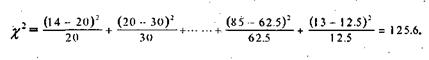
Эта величина, эта статистика знаменита тем, что имеет закон распределения, который называется законом распределения хи-квадрат. Поэтому с ее помощью решается много различных задач, про­веряются различные статистические гипотезы. Нас пока интересу­ет только аспект использования величины хи-квадрат для конструирования мер связи. Самой этой величиной как мерой свя­зи неудобно пользоваться, ибо ее значение может быть каким угод­но большим и зависит от размера таблицы сопряженности. Разли­чие в коэффициентах, основанных на хи-квадрат, заключается в определенном нормировании величины хи-квадрат. Одним из час­то используемых коэффициентов является коэффициент взаимной сопряженности Пирсона. Он имеет следующий вид:

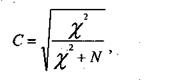
где N ¾ общее число объектов. В нашем случае объекты ¾ студенты-гуманитарии. Раньше их число мы обозначали через n₀₀, которое было равно 1000. Для наших целей так было удобнее, а в данном случае нет никакой необходимости ни в двойных индексах, ни в индексах вообще.

Если значение коэффициента получится близким к нулю или равным нулю, то это означает статистическую независимость при­знаков. Случай близости значения к единице будет говорить о ста­тистической зависимости. Значение коэффициента ни при каких условиях не достигает единицы, но для социолога это не имеет ни­какого принципиального значения. Для нашей таблицы сопряжен­ности c² =125,6, а значение С = 0,33. Опять-таки возникает вопрос о значимости отличия такого значения от нуля.

Date: 2015-09-24; view: 618; Нарушение авторских прав