Понятие детерминации

Для анализа локальной связи можно использовать и язык детер­минации [14]. Правило «если С, то У» называется детерминацией. Термин «determinatio» был введен в 1900 году в биологии и обозна­чает ситуацию, когда одно свойство («быть будущим социологом (С)») оказывает влияние на другое («быть удовлетворенным учебой (У)»). Такое влияние обозначается «С—» У». Детерминация имеет две основные характеристики: интенсивность I (С®У) детермина­ции и емкость С (С®У) детерминации. Формально — это услов­ные частоты. В наших обозначениях эти характеристики равны:

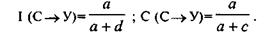
Если значения этих характеристик выразить в процентах (что очень удобно для интерпретации), то для нашего примера (см. таб­лицу 3.3.1 или первую табличку на схеме 3.4.2):

а = 60; a + d = 200; а + с = 250.

Тогда I (С®У) = 30%, а С (С®У) = 24%. Из первого значения делаем вывод, что из числа студентов, обладающих свойством С (быть социологом), 30% обладают свойством У (быть удовлетворен­ным). Интенсивность выражает как бы точность детерминации. Из значения емкости делаем вывод, что из числа студентов, обладаю­щих свойством У, 24% обладают свойством С. Емкость выражает в дополнение к интенсивности как бы полноту детерминации.

Интенсивность и емкость обладают свойствами, на основе ко­торых достаточно легко интерпретировать детерминацию. Ниже предлагается примерная схема совместной интерпретации значе­ний этих характеристик детерминации.

Схема 3.4.3. Интерпретация детерминации

Еще один способ анализа таблицы (2*2)

О статистической зависимости можно судить по таблицам, приведенным на схеме 3.4.2, и без использования коэффициентов. Ведь относительные частоты в долях (частости) являются оценками ве­роятности некоторых событий. Например, обозначим через Р(У,П)вероятность события «быть в будущем политологом и одновремен­но быть удовлетворенным учебой на четыре балла», через Р(У) ¾ вероятность события «быть удовлетворенным на четыре балла», че­рез Р(П) ¾ вероятность события «быть в будущем политологом». Известно, что если два последних события независимы, то Р(У,П)-=Р(У)*Р(П). Для нашего примера (см. таблицу 3.4.1) Р(У)=250/ 1000=0,25; Р(П)=100/1000=0,1; Р(У,П)=30/1000=0,3. Различие небольшое, поэтому события У и П, скорее всего, независимы.

Для локальной связи пригодны и любые другие меры, суще­ствующие для таблиц сопряженности любого размера (r * s), т. е. когда число строк в таблице равно r, а число столбцов равно s. Прежде чем перейти к ним, приведем пример использования на практике дихотомических пар понятий: истинное ¾ ложное значе­ние коэффициента связи; непосредственная связь ¾ опосредован­ная связь.

Date: 2015-09-24; view: 382; Нарушение авторских прав