Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Меры связи: основанные на модели прогноза и ранговые
|
|
Модальные меры Гуттмана. Сравнение распределений посредством меры Л. Гудмена и Е. Краскала. Когда социолог имеет дело с ранжированными рядами? Принцип сравнения ранжированных рядов. Связанные ранги. Коэффициенты ранговой корреляции Д. Гудмена и Е. Краскала, Р. Сомерса, М. Дж. Кендалла.
Вначале мы приведем примеры коэффициентов связи для признаков, имеющих по-прежнему номинальный уровень измерения. Особое внимание к такого рода мерам вполне оправданно. Специфика социологических данных такова, что социолог в основном работает с номинальным уровнем измерения. Исключение составляют первый (государственная статистика) и третий (бюджеты времени) типы социологической информации. Как и раньше, в качестве примера рассматриваем связь между будущей профессией студента и удовлетворенностью учебой. Это несмотря на то, что второй из них измерен по порядковой шкале. Пока эту упорядоченность никак не используем. Социологу приходится часто так поступать, ибо он всегда работает с эмпирией в ситуации разнотипности шкал. Мер, учитывающих эту разнотипность, мало, и они не всегда удовлетворяют потребностям социолога. В силу этого приходится намеренно идти на «огрубление» данных и работать в ситуации номинального уровня измерения даже тогда, когда речь идет о порядковых и «метрических» шкалах. Следует вас предостеречь. Во многих работах, упомянутых в списке литературы, содержатся разного рода неточности и некоторые ошибки в написании формул. Поэтому при самостоятельном изучении следует перепроверять формулы, сравнивая их с аналогичными из других источников.
Прежде всего рассмотрим меры, основанные на так называемой модели прогноза. Это уже как бы другой «язык» анализа таблиц сопряженности. Для социолога понятие «прогноз» носит не только многозначный характер, но к этому понятию отношение очень осторожное и трепетное. Если на основе эмпирических данных и можно что-то прогнозировать, предсказывать, то в достаточно узком смысле понимания прогноза. При этом ход рассуждений примерно такой. Если ничего не изменится, то может быть то-то и то-то. Социологи-математики (такие тоже есть) термин «прогноз, предсказание» употребляют в еще более узком смысле, но очень часто [4, 5]. Мы также будем пользоваться понятием «прогноз» в очень узком смысле. Попробуем коротко и грубо прояснить, в каком смысле.
У нас с вами есть одномерное распределение какого-то признака. Напоминаем, что под признаком понимаем как отдельно взятый эмпирический индикатор (наблюдаемый признак), так и производный от эмпирических индикаторов показатель. Пусть таковым признаком будет удовлетворенность учебой (У). Распределение этого признака можем интерпретировать следующим образом. Есть значения признака (различные степени удовлетворенности учебой), и есть вероятности этих значений (относительные частоты в долях или частости). А, точнее, оценки вероятности, полученные по выборке. Все, что рассчитывается по выборочной совокупности, называется оценками истинных (существующих для изучаемой генеральной совокупности) значений. Разумеется, социолог может опускать термин «оценка», если понимает, о чем идет речь. Для простоты мы будем поступать так же.
Итак, наши вероятности P0j равны маргинальным частотам по столбцам (именно они соответствуют признаку (У) ¾ удовлетворенность учебой), деленным на общее число опрошенных студентов-гуманитариев (n00). В виде формулы это выглядит так: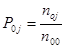 
. Тогда, по приведенной ниже таблице 3.5.1 (это та же таблица сопряженности, с которой мы постоянно работаем), вероятности пяти степеней удовлетворенности учебой равны:
Эти вероятности можно интерпретировать как вероятности статистического предсказания (У). Мы же их получили по «хорошей» выборке. Поэтому если из нашей изучаемой генеральной совокупности студентов-гуманитариев случайно выберем некоторого студента, то вероятность того, что у этого случайного студента окажется максимальная удовлетворенность учебой, очень мала. Это потому, что по выборке она была равна всего лишь 0,05. Вероятность «отгадать» все остальные варианты удовлетворенности учебой тоже невелика ибо они, как видите, не больше, чем 0,3. При этом само понятие «вероятность» можно трактовать на уровне обыденного сознания. Только в повседневной жизни вам обычно говорят, например, «вероятность того, что у меня завтра будет плохое настроение для прогулки, равна 90%» или «вероятность того, что я завтра приду к тебе в гости, меньше 50%» или «вероятность нашей возможной встречи «фифти - фифти» (50 на 50)». И вы всегда понимаете, что сие означает. При этом такие суждения вы интерпретируете не столько количественно, сколько качественно. А в математических формулах пользуются не процентами для оценки вероятности, а долями ¾ частостями — и, соответственно, вероятность принимает вполне конкретное значение из интервала от 0 до 1.
Теперь вполне правомерно поставить вопрос: Как изменятся рассчитанные нами вероятности иметь ту или иную степень удовлетворенности учебой, если привлечь к анализу второй признак (будущую профессию студента)? Можно вопрос поставить и по-другому: Насколько знание будущей профессии прибавит знания об удовлетворенности учебой? Или: Насколько информация о будущей профессии изменит информацию об удовлетворенности учебой? Поиск ответа на последний вопрос порождает меры связи, основанные на понятии энтропии (мы касались этого понятия при введении качественных коэффициентов вариации). Такого рода меры мы не будем рассматривать. Вы можете с ними познакомиться в работах [3, 8, 11].
Первый наш вопрос можно поставить и так: Как и насколько изменятся вероятности предсказания удовлетворенности учебой, если учесть будущую профессию? Как вы уже догадываетесь, по сути речь идет о знании условных распределений нашего признака (У) или условных частот, или условных вероятностей, т. е. вероятностей, которые логично обозначить как Р.... Индекс первый (j) относится к столбцам, т. е. к удовлетворенности учебой (признак У), второй (i) относится к строкам, т. е. к будущей профессии (признак X), а косая черта подчеркивает, что признак (X) является условием.
Существуют всевозможные коэффициенты, помогающие найти ответ на подобные вопросы. Как видно из наших рассуждений, они должны быть направленными и носить, так же как и меры, основанные на хи-квадрат, характер «глобальный», т. е. давать оценку связи в целом для всей таблицы сопряженности в отличие от локальных мер (связь отдельных свойств).
Если для кого-то термин «предсказание» остался пока непонятым, то при описании предлагаемых ниже мер как можно реже будем пользоваться этим термином.
Меры l (лямбда) Л. Гуттмана (L. Guttmann)
Таких мер три, две из них направленные, а одна представляет собой усреднение первых двух. Мы приведем только одну lу/х. Эта мера, этот коэффициент характеризует в случае нашей задачи влияние будущей профессии (X) на удовлетворенность учебой (У). Отвечает на вопрос, насколько изменяется предсказание (У) при знании (X). Ниже приводится формула, в которой используются известные вам обозначения, за исключением:
niшах ¾ максимальная частота в i-й строке:
nотах ¾ максимальная частота среди маргинальных частот по столбцам.
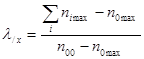
Эта формула была бы понятнее, если вместо частот использовать частости (доли), интерпретируемые как вероятности [11, с. 126]. Такую формулу мы не будем приводить, чтобы не пугать излишними формулами. Отметим лишь, что в литературе приводится как формула, записанная через абсолютные частоты, так и через частости. Кроме того, фамилия Гуттмана тоже приводится по-разному. Например, Гудман в работе 8, с. 131. Это не так уж важно.
Для того чтобы пояснить содержательный смысл этой меры, этого коэффициента, ниже приводится та же таблица сопряженности, с которой мы постоянно работаем для изучения взаимосвязи между «будущей профессией студента» (признак X) и «удовлетворенностью учебой» (признак У). Таблица 3.5.1 содержит те же частоты, что и таблица 3.3.1, за исключением обозначений самих частот. В нее добавлен новый столбец ¾ последний с максимальными частотами по всем строкам, включая строку с маргинальными частотами по столбцам. Они нам необходимы для вычисления коэффициента lу/х Гуттмана.
Чему же равен коэффициент в нашем случае? Он рассчитывается очень просто.
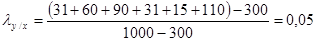
Даже по тому, как вычисляется коэффициент, видно, что он позволяет определять, существуют ли в строках модальные группы, т. е. есть ли в каждой профессиональной группе ярко выраженная, часто встречаемая «степень удовлетворенности учебой». Судя по нашей таблице, таких групп практически нет, что и подтверждается маленьким значением коэффициента. Какими же свойствами обладает этот коэффициент?
1. Он изменяется от нуля до единицы.
2. Он равен единице только в одном случае, когда в каждой профессиональной группе все студенты имеют одинаковую степень удовлетворенности учебой и при этом в каждой отличную от другой. Если бы наша таблица сопряженности при тех же маргинальных частотах имела бы такой вид, как это представлено в таблице.3.5.2, коэффициент был бы равен 0,86.
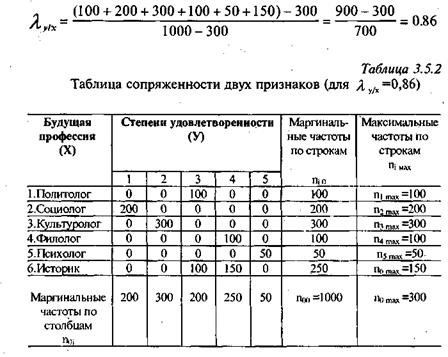
Итак, визуально мы наблюдаем наличие модальных групп в строках, кроме последней. Если бы в нашей таблице число строк равнялось числу столбцов, например, не было бы историков, то коэффициент был бы равен 1, а таблицу можно было бы перестановкой столбцов превратить в такую, в которой только диагональные элементы отличались бы от нуля. Таким образом, по значению коэффициента можно судить о степени отличия реальной таблицы от диагональной. В случае, когда значение коэффициента равно 1, вероятность статистического предсказания (У) по X максимальная. Такой случай практически в социологических исследованиях не встречается.
3. Значение коэффициента равно нулю в нескольких случаях. Первый ¾ все частоты сосредоточены только в одной строке. На самом деле знание признака X нечего не дает для увеличения знания об У. Второй случай ¾ отсутствие феномена модальности, т. е., условно говоря, полная «размытость» данных в таблице. По таблице 3.5.1 мы получили значение, близкое к нулю и равное 0,05. Практически модальность не наблюдается. И наконец, третий случай, когда все частоты сосредоточены только в одном столбце.
Этот случай заслуживает особого внимания, ибо противоречит основному содержанию коэффициента. Если данные сосредоточены в одном столбце, то естественно модальные классы существуют. Тогда и вероятность предсказания значения У по значению X должна быть равна единице. А наш коэффициент равен нулю. Здесь мы наблюдаем ситуацию, когда коэффициент плохо ведет себя в нуле. Запомните эту фразу. Вы будете встречаться с подобными фразами и в случае других коэффициентов. Чтобы исключить неверную интерпретацию нулевого значения, необходимо по одномерному распределению уточнить, не сосредоточены ли данные только в одном столбце. Такой случай также не встречается в социологической практике.
Представляется важным отметить, что в реальных исследованиях значения коэффициента Гуттмана очень малы и использовать их нужно так же, как и многие другие коэффициенты в сравнительном контексте, например, для ранжирования как бы независимых между собой признаков по степени их влияния на некоторый особенно важный для исследователя признак, обозначаемый как целевой, зависимый. Если такого нет, то направленные коэффициенты «лямбда» использовать не имеет особого смысла.
Меры t (may) Л. Гудмена и Е. Краскала (L. Goodman, Е. Kruskal)
Эти меры, на мой взгляд, интересны социологу, ибо с ними можно работать в сравнительном контексте, не обращая особого внимания на всякие значимости. Таких мер вообще-то три, как и в случае мер Гуттмана. Первые две из них направленные, а третья как бы усредняет первые два. Мы рассмотрим только одну из них. Для этого опять обратимся к нашей таблице сопряженности 3.5.1. При этом вспомним и рис. 3.3.1. На этом рисунке были изображены эмпирические кривые распределения удовлетворенности учебой в каждой профессиональной группе ¾ будущие профессии студентов-гуманитариев (мы уже обозначили эти признаки через У и X). Визуально мы с вами наблюдали наличие трех типологических синдромов по характеру распределения признака У. Другими словами, три типа структуры удовлетворенности учебой.
Ни один коэффициент глобального характера не позволит определить, сколько типов структур наблюдается. Если социолога интересуют такие группы, то до применения всяких коэффициентов представляется целесообразным хотя бы визуально на компьютере просмотреть графики такого вида, которые изображены на рис. 3.3.1 и рис. 3.3.2. Тот же коэффициент, который мы рассмотрим, позволяет в целом определить степень отличия условных распределений У от безусловного. Ниже приведем формулу. В ней будем использовать обозначения вероятностей (условных и безусловных), введенных в начале этого раздела. В этот раз формулу запишем не на языке абсолютных частот, а на языке вероятности ¾ доли, частости. В литературе она приводится обычно через абсолютные частоты [1, с. 36, 3, с. 36].
Один из грех коэффициентов т (may) Гудмена и Краскала выглядит следующим образом.
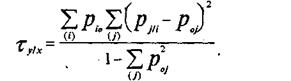
Если вы подставите в эту формулу вместо вероятности (точнее оценок вероятности) частоты, то получите формулу, приводимую в литературе, т. е.:
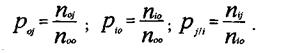
Две первые формулы служат для вычисления безусловных вероятностей. Их значения приведены соответственно в последней строке таблицы 3.5.3 и в последнем столбце. Третья формула — для вычисления условной вероятности. Значения такой вероятности приведены в ячейках таблицы 3.5.3. Они аналогичны данным таблицы 3.3.2 (верхнее левое значение в ячейках).
Таблица 3.5.3
Таблица сопряженности (условные и безусловные вероятности)
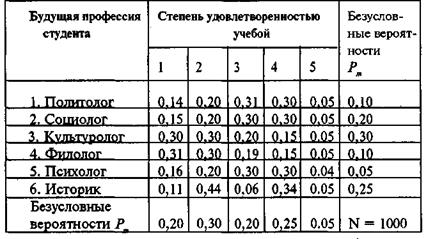
Коэффициент «t» чем-то напоминает и «хи-квадрат», и l Гуттмана. Однако он не такой «прозрачный» для объяснения, как эти коэффициенты. Вообще-то говоря, если все можно было бы описывать и объяснять в социологии вербально, то, может, язык математики был бы и не нужен. И что совершенно очевидно, чем ближе язык математики к языку социолога, тем он сложнее. Все таки попытаемся прояснить содержательный смысл приведенного коэффициента.
Прежде всего необходимо пояснить, зачем при сравнении распределений всякие квадраты. В числителе квадрат по аналогии с формулой дисперсии. Для того чтобы учесть отклонение условной частоты от безусловной в одну и другую сторону. В знаменателе сумма квадратов безусловных вероятностей. Простая их сумма всегда равна единице. Это вы знаете. Такой знаменатель ¾ количественная характеристика распределения по столбцам (безусловное распределение по У). Числитель несет в себе основное содержание коэффициента. В числителе в скобках ¾ отклонение условной вероятности от безусловной вероятности У. Естественно, все отклонения суммируются по всем значениям У (по всем столбцам). В свою очередь такие величины, полученные по каждой строке (по каждому условному распределению У) суммируются как бы с весами, равными безусловной вероятности по строке. Тем самым строки уравниваются в «правах» за вклад в значение коэффициента. Напомню, что при вычислении величины «хи-квадрат» мы уравнивали в «правах» ячейки таблицы сопряженности, а здесь ¾ строки.
Коэффициент t (may) Гудмена и Краскала обладает следующими свойствами:
1. Принимает значение от нуля до единицы.
2. Равен нулю, если структура распределения по строкам одинакова и такая, как структура распределения маргинальных (по столбцам) частот. В этом случае наблюдается статистическая независимость У от X. Будущая профессия не влияет на удовлетворенность учебой.
3. Равен единице, если будущая профессия студента полностью детерминирует его удовлетворенность учебой. Каждой профессии соответствует своя собственная степень удовлетворенности учебой. Чисто формально это означает, что таблицу сопряженности можно привести к диагональному виду. В самом деле, для таблицы 3.5.2 значение коэффициента равно t y/х = 0,83
Вычислим значение коэффициента для нашей таблицы 3.5.3. Чтобы вычислить числитель, нужно сложить 6 (для всех строк таблицы) величин. Каждая такая величина равна
Тогда значение коэффициента будет равно tу/х = 0,03. Такое небольшое значение коэффициента говорит об отсутствии влияния будущей профессии на структуру удовлетворенностью учебой. Вероятность предсказания удовлетворенности учебой практически не изменится, если учитывать будущую профессию.
До сих пор мы с вами рассматривали только меры связи для номинальных признаков, ибо они чаще других встречаются в социологических данных. При этом, анализируя данные нашей таблицы сопряженности, мы не обращали внимания на то, что один из признаков имел порядковый уровень измерения. Не использовать информацию об упорядоченности ¾ значит намеренно отказаться от ценной информации. Разумеется, существуют коэффициенты, позволяющие учесть то, что один из сопрягаемых признаков измерен по порядковой шкале.
Существует так называемый ранговый бисериальный коэффициент для случая изучения связи между дихотомическим (поэтому коэффициент называется бисериальным) номинальным признаком и ранговым [2, с. 165—167, 8, с. 139, 11, с. 121]. При этом для случая несвязанных рангов. Напомним, что с ситуацией связанных рангов мы встречаемся, если в ранжированном ряду есть одинаковые ранги. Также существует точечный бисериальный коэффициент для случая изучения связи между дихотомическим номинальным признаком и «метрическим».
Date: 2015-09-24; view: 592; Нарушение авторских прав