Задание на семинар или для самостоятельного выполнения. 1. На основе той же самой матрицы данных составить таблицу сопряженности между первым (номинальная шкала) и вторым (порядковая шкала) признаками

1. На основе той же самой матрицы данных составить таблицу сопряженности между первым (номинальная шкала) и вторым (порядковая шкала) признаками. В каждой ячейке таблицы под­считать значение четырех показателей: абсолютную частоту и от­носительные частоты в долях (частости) по всем объектам, по строке и по столбцу.

2. На одном и том же рисунке построить эмпирические кри­вые распределения по первому признаку для различных групп объектов, выделенных по отдельным значениям второго признака. Сравнить эти кривые и сделать выводы о характере связи двух признаков, о наличии типологических синдромов.

3. На одном и том же рисунке построить эмпирические кри­вые распределения по второму признаку для различных групп объектов, выделенных по отдельным значениям первого призна­ка. Сравнить эти кривые и сделать выводы о характере связи двух признаков, о наблюдаемых эмпирических закономерностях.

4. МЕРЫ СВЯЗИ, ОСНОВАННЫЕ НА ПОНЯТИЯХ «СТАТИСТИЧЕСКАЯ ЗАВИСИМОСТЬ» И «ДЕТЕРМИНАЦИЯ»

Две логические схемы использования коэффициентов связи. Локаль­ные меры связи для таблиц сопряженности. Коэффициент Юла. Понятие детерминации. Интенсивность и емкость детермина­ции. Оценки вероятности. Истинное ¾ ложное значение мер связи. Понятие о величине c² (хи-квадрат). Коэффициент взаимной со­пряженности Е. Пирсона. Значимость значений коэффициентов связи. Доверительный интервал.

Рассмотренные дихотомические пары понятий, составляющие контекст для эмпирической интерпретации понимания связи, есте­ственным образом привели нас к выводу о необходимости суще­ствования большого количества коэффициентов парной связи. Каж­дая мера связи (каждый коэффициент связи) вводится таким образом, чтобы его значения изменялись либо от нуля до единицы, либо от минус единицы до единицы. Это единственное, что объединяет все коэффициенты. Перед социологом всегда стоит трудный вопрос, связанный с тем, как понимать связь и какой коэффициент выб­рать для изучения взаимосвязи между признаками. Иногда возни­кает иллюзия, что, получив значения всевозможных коэффициен­тов и сравнив эти значения между собой, можно сделать достоверный вывод о силе связи между признаками. Дело в том, что сравнивать имеет смысл только коэффициенты, основанные на одном и том же понимании связи.

Обычно раздражение социолога-пользователя вызывает и то, что нельзя сравнивать силу связи в разных исследованиях по значениям коэффициентов. Если в одном исследовании коэффи­циент равен 0,5, а в другом тот же коэффициент для тех же признаков 0,6, нельзя утверждать, что второе больше первого. Ведь социолог, анализируя связь, всегда ищет ответы на вопросы: «Насколько влияет/не влияет...?», «Насколько зависит/не зави­сит...?». Коэффициенты же зачастую на эти вопросы не отвечают. У них свой язык понимания связи, который необходимо понять. Только тогда появляется возможность использования их для отве­та на подобные вопросы.

Для того чтобы правильно пользоваться каким-нибудь коэффи­циентом, необходимо прежде всего знать все его возможности и не требовать от него того, чего он не может дать социологу. В социо­логических исследованиях сами значения коэффициентов, как пра­вило, бывают маленькими. Наблюдается такая странная картина, когда все анализируемые признаки друг с другом связаны, но очень слабо (по значениям мер взаимосвязи). Почему это происходит ¾ понятно. Мыс помощью парных связей рассматриваем непосредственные связи между двумя признаками, а в социологии все опос­редовано. Другими словами, на нашу пару признаков влияют мно­жество других. Что это за признаки, не всегда известно. Поэтому использование отдельно взятого коэффициента эффективно только в сравнительном контексте и только в рамках одного исследования. Например, возможны две логические схемы использования парных коэффициентов связи.

Первая состоит в следующем. Из всей совокупности призна­ков, связи между которыми интересуют социолога, выделяется ка­кой-то важный, главный, зависимый, целевой признак, и рассматри­ваются его парные связи с остальными. В самом простом случае последние считаются как бы независимыми друг от друга и влияю­щими в разной степени на целевой. Вычисляются значения коэф­фициента и по этим значениям проводится процедура ранжирова­ния всех независимых признаков по степени их влияния на целевой. Затем на основе сугубо качественного анализа отбираются из неза­висимых наиболее тесно связанные с целевым. Этот прием чисто практический и теоретически может быть и необоснован. К сожа­лению, социологу на каждом шагу приходится идти на подобные нарушения. Такая логическая схема анализа может вывести социо­лога к необходимости формирования новых гипотез о причинно-следственных отношениях между признаками.

Вторая схема возникает в ситуации невозможности (содержа­тельной бессмысленности) выделения целевого из всей совокуп­ности анализируемых признаков. Тогда вычисляются значения ко­эффициента связи для всевозможных пар признаков. С помощью задания некоторого порога (значения коэффициента) отсекаются все связи со значением коэффициента, который меньше этого порога. Строится граф структуры взаимосвязей, где вершины ¾ признаки, а ребра ¾ связь между ними. Пусть у нас с вами каких-то шесть признаков и вычислены значения какого-то коэффици­ента. На рис. 3.4.1 и на рис. 3.4.2 приведены два графа.

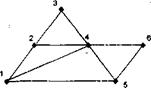
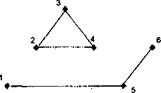
Рис. 3.4.1 Граф связи Рис. 3.4.2 Граф связи

Первый из них получился с большим количеством связей, по­тому что задали маленькое значение порога. Второй граф получил­ся с очень маленьким числом связей, потому что задали большое значение порога. Значения коэффициентов не имеет особого смыс­ла приводить. Нам важен только содержательный смысл этой про­цедуры. На первом графе могут быть изображены и несуществен­ные связи, а во втором наоборот ¾ существенные могли быть потеряны. Независимо от содержания признаков, принцип выбора порога всегда носит итеративный характер и критерии всегда каче­ственные. Такая логическая схема может вывести социолога к формированию гипотез о социальных факторах. Ибо на втором графе наблюдаем, к примеру, два факторных синдрома, т. е. две группы взаимосвязанных признаков, что является основой для формирова­ния индексов.

Date: 2015-09-24; view: 294; Нарушение авторских прав