Признак Лейбница

Если для знакочередующегося числового ряда

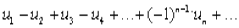(19)

Выполняются два условия:

1. Члены ряда убывают по модулю u₁ > u₂ >…> u_n >…,

2.

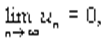
то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда.

Следствие. Остаток ряда Лейбница имеет знак своего первого члена и меньше его по абсолютной величине, т.е.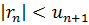

Если в знакочередующемся ряде члены ряда монотонно убывают по абсолютным значениям и imU_n=0 (nà∞), то ряд сходится.

Дано: U₁>U₂>U₃>...; imU_n=0 (nà∞); U₁-U₂+U₃-U₄+..., U_i>0

Доказательство: S_2n ¾ чётная частичная сумма:

S_2n=+U₁-U₂+U₃-U₄+...-U_2n;

S_2n=(U₁-U₂)+(U₃-U₄)+...+(U_2n-1-U_2n);

S_2n>0 ¾ возрастает.

S_2n=U₁-(U₂-U₃)-(U₄-U₅)-...-U_2n; S_2n<U₁, U₁>0; imS_2n=S {nà∞}

imS_2n+1 {nà∞} = im(S_2n+U_2n+1)=S;

Чётные и нечётные суммы с одним пределом => ряд сходится.

1) Заметим, что S>0, т.е. знак суммы совпадает со знаком первого члена.

2) S<U₁

38. Абсол и условная сходимость.

О. Ряд вида 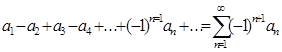(1)

наз знакочеред-ся.

Признак Лейбница (сх-ть знакочер ряда).

Для того, чтобы ряд (1) сх-ся достаточно, чтобы абсол значения убывали и →0 при возрастании n, т.е.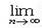

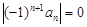
О. Если ряд, сост из абсол значений величин 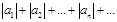сх-ся, то ряд 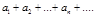наз абсолютно сходящимся.

Теорема: Если ряд явл абсол сх-ся, то исх ряд сх-ся.

Док-во:восп-ся 1 признаком сравнения

Рассм-м ряд 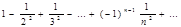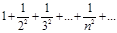- ряд из абсол значений величин

Доказана сх-ть по 2-му признаку сравнения, след-но исх ряд сх-ся абсолютно.

О. Если ряд, образ из абсол значений его величин расх-ся, а исх ряд сх-ся, то он наз условно сх-ся.

39. Понятие степенного ряда. Область сходимости степенного ряда. Теорема Абеля.

Ряд вида 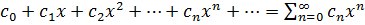, где 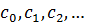- числа, называемые коэффициентами ряда, x – переменная, наз-ся степенным рядом. Интервал (-R;R) наз интервалом сх-ти степ ряда. Заметим, что для x €(-R;R) ряд сходится абсолютно, а в точках x= ± R степенной ряд может сходиться или расходиться. Для нахождения радиуса сходимости можно воспольз-ся, признаками Даламбера или Коши. Теорема. Если существует 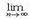| a_n+1/ a_n|=L, то R=1/L= 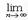| a_n/ a_n+1|. (Док-во. Рассмотрим ряд 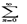a_nxⁿ. Применим к нему признак Даламбера. 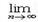| a_n+1xⁿ⁺¹/ a_nxⁿ|= 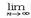| a_n+1/ a_n|∙| x | =L∙| x |. Отсюда следует, что если L∙| x |<1, т,е. если | x |<1/L, то ряд сходится абсолютно. Если L∙| x |>1, то ряд расходится. Теорема доказана.) Заметим, что если L=0, для любого | x | то R=∞. Если L=∞, для любого x≠0, то R=0. Если R=0, то ряд сходится в единственной точке x₀=0; если R=∞, то ряд сходится на всей числовой прямой. Итак, интервал сходимости ряда 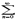a_nxⁿ есть (-R;R). Для нахождения области сходимости ряда надо отдельно исследовать сходимость в точках x=R и x=-R; в зав-ти от рез-тов этого исслед-я обл-ю сх-ти ряда м. б. один из промежутков: [-R;R],(-R;R),[-R;R),(-R;R]. Теорема Абеля: 1) Если степенной ряд 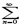a_nxⁿ сходится при x=x₀, то он сходится причем абсолютно для всех x, удовлетворяющих неравенству |x|<|x₀|. 2) Если же ряд 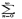a_nxⁿ расходится при x=x_1, то он расходится при всех x, удовлетворяющих условию |x|>|x₁|. (Док-во 1)Так как числовой ряд 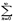a_nx₀ⁿ сходится, то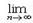 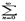a_nx₀ⁿ=0. Это означает, что числовая последовательность {a_nx₀ⁿ} ограничена.Тогда перепишем степенной ряд в виде a₀ + a₁x₀ (x/x₀) + a₂x₀²(x²/x₀²) +…+…= 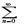a_nx₀ⁿ (x/x₀)². Рассмотрим ряд из абсолютных величин. |a₀| + |a₁x₀ (x/x₀) | + |a₂x₀²(x²/x₀²) | +…+…<= M + M| x/x₀| + M| x/x₀|² +…= M(1+q+ q²+…). Это геометрическая прогрессия с q=(x/x₀)<1—сходится. Из признака сравнения следует абсолютная сходимость степенного ряда. 2)От противного. Пусть степенной ряд сходится при некотором x^*, | x^*|> x_1. Но тогда согласно 1-ой части теоремы, степенной ряд сходится для всех | x |< x^*. В том числе должен сходится и при x= x₀, так как | x |< | x^*|. Но это противоречит предположению теоремы. Теорема доказана.)

Date: 2015-09-05; view: 772; Нарушение авторских прав