Диф уравнение с разделяющимися переменными. Однородные диф уравнения

Уравнения с разделяющимися пере­менными. называется дифференциальное уравнение вида f(x)dx + g(y)dy = 0 с непрерывными функциями f(х) и g(y).

Равенство 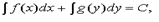где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.

Начальное условие для уравнения f(x)dx + g(y)dy = 0 можно задавать в виде y(x0) = y0 или в виде x(y0) = x0.

Уравнением с разделяющимися переменными называется дифференциальное уравнение вида f1(x)g1 (y)dx + f2(x) g2(y)dy =0.

Функции f1(x), g1(y), f2(x), g2(y) непрерывны в cвоих областях определения и g1(y)f2(x) ≠ 0.

Разделив обе части уравнения на отличное от нуля произведение g1(y)f2(x), получим уравнение с разделенными переменными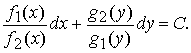

Общий интеграл этого уравнения имеет вид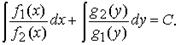

27. ЛДУ 1-го порядка (вывод формулы общего решения)

ДУ вида A(x)y’+B(X)y+C=0, где A(x)≠0, или после деления на A(x), приведённое к виду y’+p(x)y=q(x), называется линейным ДУ первого порядка. Если q(x) 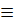0, то уравнение называется линейным однородным, иначе – линейным неоднородным.

Линейное однородное уравнение – это уравнение с разделяющимися переменными, его общее решение выражается формулой .

Для решения линейного неоднородного уравнения можно применять метод вариации произвольной постоянной, тогда общее решение неоднородного уравнения получается в виде .

y(x) = u(x) v(x): из этого выражения находим u(x), и y(x) = u(x) v(x).

Линейное неоднородное уравнение может быть сведено к решению двух уравнений с разделяющимися переменными при помощи подстановки(метод Бернулли)y(x) = u(x) v(x) двух неизвестных дифференцируемых ф-и й u(x) и v(x).Тогда 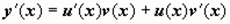, и уравнение приводится к виду 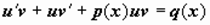, или .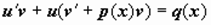

Найдем функцию v(x) как некоторое ненулевое частное реш-е однородного ур-я 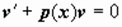. затем находим u(x) из уравнения 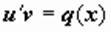. после нахождения v(x) определяем u(x) как реш-е ур-я 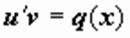. тогда 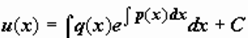. отсюда реш-е линейного неоднородного ур-я сводится к реш-ю двух ур-ей с раздедяющимися переменными и имеет вид .

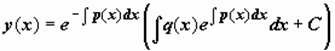28,29. Линейные диф ур-я второго порядка с пост коэф­фициентами. имеет вид

Линейным однородным уравнением второго порядка называется уравнение 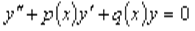. Уравнение 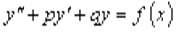будем называть линейным неоднородным уравнением.

Общее реш-е линейного однородного диф.ур-я имеет вид: y=C₁y₁(x)+C₂y₂(x)

Для неоднородного линейного ур-я общее реш-е имеет вид:y= C₁y₁(x)+C₂y₂(x)+µ(x)

Еслиp(x)≡p, q(x)≡q – постоянные, то линейное ур-е 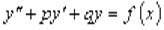называется уравнением с постоянными коэффициентами и записывают его так: 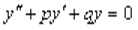. Для нахождения y₁(x), y₂(x)этого ур-я при f(x)=0 составляет квадратноеур-е λ²λ+pλ+q=0, кот-е назыв. характеристическим.

Возможны 3 вар-та:

D>0 корни ур-яλ_1, λ₂различные. Общее реш-е однородногоур-я y=C₁e^λ₁^x+C₂e^λ₂^x

D=0 корниλ₁₌λ₂₌λодинаковые. тогдереш-е y=e^λx(C₁+C₂x)

D<0 корни ур-я λ_1,2=α^+/-iβ(i=корень из -1). реш-е y=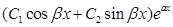

30. Лин неоднор ДУ 2-го порядка с пост коэфф-ми.

Рассмотрим уравнение y´´+py´+qy=r(x) /где p,q € R, r(x)-функция.

которое имеет вид y=yO+yЧ, где

yO-общее решение уравнения y´´+py´+qy =0

yЧ-частное решение уравнения y´´+py´+qy=r(x), которое зависит

от вида правой части,т.е r(x)

Рассмотрим некоторые частные случаи:

1) r(x)=Pn(x),где Pn(x) – многочлен степени «n»

В этом случае решение yЧ ищут из уравнения к²+pк+q=0 в виде:

• yЧ=Qn(x) при q≠0

• yЧ=x Qn(x) q=0, p≠0

• yЧ=x² Qn(x) q=p=0

2) r(x)=а 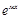где а,м € R, а,м =соnst

Вид частного решения следущее:

• yЧ=А 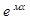если «м» не явл корнем Ур-я к²+pк+q=0

(корни некратные,некомплексные)

• yЧ=Аx 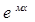если «м» –простой корень ур-я к²+pк+q=0

•yЧ=Аx² 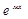если «м»-кратный корень Ур-я к²+pк+q=0

3) r(x)=acosmx+bsinmx где a,b,m=const

• yЧ= Acosmx+Bsinmx при условии что p²+(q-m²)≠0

• yЧ= x(Acosmx+Bsinmx) если p²+(q-m²)=0, p=0,q= m²

Date: 2015-09-05; view: 466; Нарушение авторских прав