Интеграл с бесконечными пределами и от неограниченной ф-ии

Интегралы с бесконечными пределами интегрирования и интегралы от неограниченных ф-ций газ несобственными интегралами.

Пусть ф-я 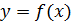непрерывна на промежутке 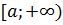и интегрируема на любом конечном его отрезке 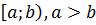. Тогда несобственным интегралом с бесконечным верхним пределом наз предел 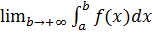, к-й обознач символом 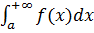, т.е. 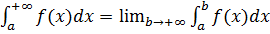Если предел сущ и конечен, то несобственный интеграл наз сходящимся, в противном случае – расходящимся.

Аналогично опред несобств интегралы на промежутке и :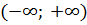

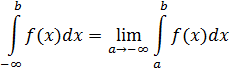
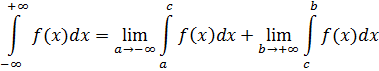
Если сходятся оба интеграла в правой части последней формулы, то интеграл 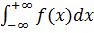наз сходящимся, и расходящимся, если хотя бы 1 из них расходится. Если f(x) непрерывна для всех х отрезка [a,b], кроме точки с, в к-й f(x) имеет разрыв II рода, то по определению имеет разрыв II рода, то по определению 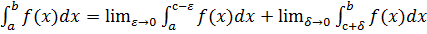, где 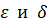изменяются независимо друг от друга.

Несобственный интеграл 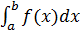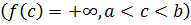наз сходящимся, если оба предела в правой части равенства существуют, и расходящимся, если не существует хотя бы 1 из них.

В случае с=а или c=b получаем 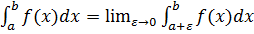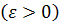, или 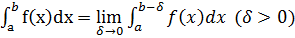. При исследовании сходимости несобств инт-ов пользуются одним из признаков сравнения. 1) Если ф-ии f(x) и 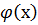определены на промежутке [a; + 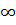), интегрируемы на отрезке [a,A], где A 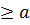и 0 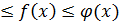для всех x 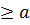, то из сходимости интеграла 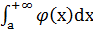следует сх-ть интеграла 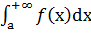, а из расходимости интеграла 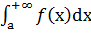вытекает расх-ть инт-ла 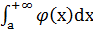. (признак сравнения). 2) Пусть на промежутке [a; + 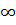) определены 2 положительные функции f(x) и 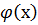, инт-емые на любом конечном промежутке [a,b]. 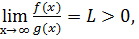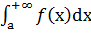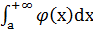Тогда, если существует конечный предел то интегралы и сходятся и расх-ся одновременно (предельный признак сравнения). 3)Если интеграл 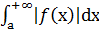сходится, то сходится и инт-л 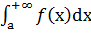. В этом случае инт-л 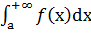называется абсолютно сходящимся. 4) Если при x -> + 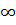ф-я f(x)>0 является бесконечно малой порядка 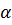по сравнению с 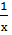, то интеграл 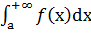сходится при 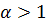и расходится при 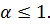На практике часто для сравнения используется ф-ия 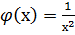. Известно, что 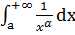сходится при 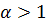и расх-ся при 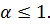Аналогичные признаки сх-ти можно указать и для инт-ов от разрывных ф-ий. Для сравнения в признаке 4) используют инт-л 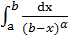( 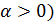или 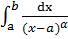, который сходится при 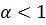и расх-ся при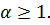

Date: 2015-09-05; view: 387; Нарушение авторских прав