
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные свойства сходящихся и несходящихся рядов
|
|
Сходящихся:
1. Отбрасывание конечного числа членов ряда (или добавление к ряду конечного числа членов) не влияет на сходимость или расходимость этого ряда.
2. Сумма сход числ ряда умнож на const равно его сумме умнож на ту же const. 
3. Если числ ряды 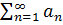 и
и 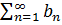 сходятся, то сумма этих числ рядов также явл сход числовым рядом, при этом его сумма равна сумме исходных рядов:
сходятся, то сумма этих числ рядов также явл сход числовым рядом, при этом его сумма равна сумме исходных рядов: 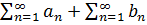 =
= 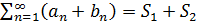
Сходимость ряда, составленного из членов геометрической прогрессии. Ряд, составленный из членов геометрической прогрессии со знаменателем q и с первым членом a1, a1≠0, вида a1+a1q+a1q2+…+a1qn-1+…= 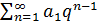
Частичная сумма ряда 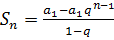 , a1≠0, q≠1
, a1≠0, q≠1
Рассмотрим 4 случая
1. При 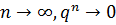 (так как | q |<1), поэтому
(так как | q |<1), поэтому 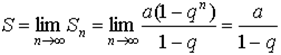
и ряд будет сходящимся.
| 2. Если q = 1, то ряд имеет вид a1 + a1 + a1 + a1 +... + a1 +.... |
Сумма Sn первых его n членов, равная na, при 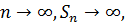 Таким образом, ряд расходящийся.
Таким образом, ряд расходящийся.
3. Если q = -1, то ряд примет вид
a1 – a1 + a1 – a1 + a1- a1 +... +(-1)n-1 a1 +.... Его частичные суммы попеременно будут равны то 0, то a1, в зависимости от того, будет ли n четным или нечетным числом. Очевидно, что при 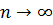 частичные суммы частичные суммы 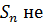 стремятся ни к какому пределу. Ряд расходится стремятся ни к какому пределу. Ряд расходится
|
4. Если | q |>1, тогда 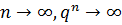 и, следовательно,
и, следовательно, 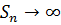 , поэтому ряд является расходящимся и суммы не имеет
, поэтому ряд является расходящимся и суммы не имеет
Date: 2015-09-05; view: 611; Нарушение авторских прав