Вычисление площадей с помощью определенного интеграла(в прямоугольной и полярной системе координат)

ПЛОЩАДИ ПОВ-ТЕЙ ТЕЛ ВРАЩЕНИЯ: 1) y=f(x) непрерывна на отрезке [a,b ] – в случае вращения графика этой ф-ии: S= 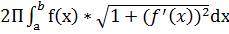; 2) В случае параметрического задания дуг кривой: x=x(t), y=y(t), t[t1,t2]

S= ; 3) В случае задания дуги кривой уравнением r=r(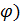 в полярных координатах .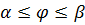

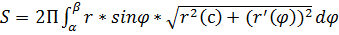22. ОБЪЕМ ТЕЛА ВРАЩЕНИЯ: Пусть функция y=f(x) непрерывна на отрезке [a,b ]. В этом случае объем тела, образованного вращением около оси 0x криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми x=a, x=b и осью абсцисс, может быть найден по формуле: 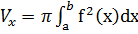. Если вращение происходит вокруг оси 0у, то объем тела вращения находится по формуле: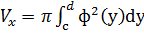

23. ДЛИНА ДУГИ: Под длиной дуги понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, при условии, что количество звеньев ломаной линии неограниченно возрастает, и при этом длина наибольшего звена ломаной стремится к нулю. Если дуга задана непрерывно дифференцируемой функцией y=f(x), то ее длина l вычисляется по формуле: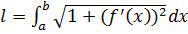

Date: 2015-09-05; view: 500; Нарушение авторских прав