Основные свойства определенного интеграла(с док-вом)

1) Если f(x) и g(x) 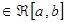, 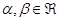- произвольные числа, то функция 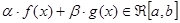и справедливо равенство: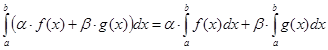

2) Если f(x) 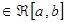, то

3) Если f(x) 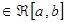и c 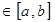, то f(x) 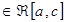, f(x) 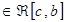и справедливо равенство: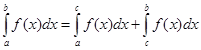

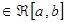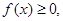
4) Если f(x) , 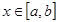и b>a, то справедливо неравенство: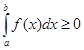

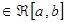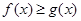
5) Если f(x) и g(x) , 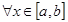и b>a, то справедливо неравенство:

6) Если f(x) 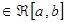и 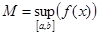, , 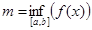b>a, то выполняются неравенства: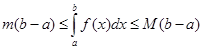

7) Если f(x) 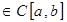, то 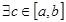, такое, что выполняется равенство: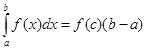

Доказательство свойств.

1) 1) Напишем интегральную сумму для функции .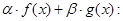
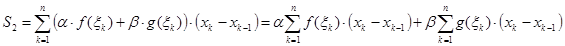Обозначим 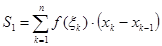и .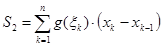
Тогда получим равенство: .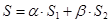
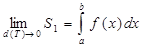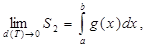Так как и то 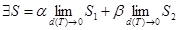и по определению он равен 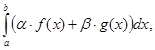что и доказывает свойство 1.

2) Напишем интегральную сумму для f(x): .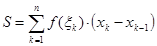
Обозначим 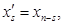s=0,…,n и 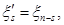s=1,…,n.

Тогда 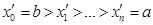и .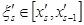

В интегральной сумме S заменим k=n-s:

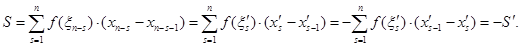
По определению 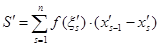есть интегральная сумма для интеграла 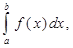что и доказывает свойство 2.

3) Без доказательства.

4) Из неравенства: 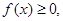b>a, следует, что 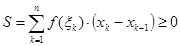и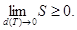

5) Так как 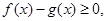то из свойств 1 и 4 следует, что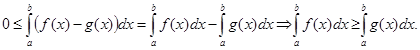

6) Так как 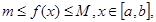то интегрируя эти неравенства, ввиду свойства 5, получим: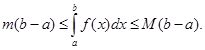

7) Так как f(x) 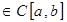, то f(x) 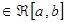(это будет доказано в следующем параграфе).
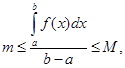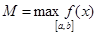Из свойства 6 следует, что где и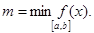
По теореме о промежуточном значении непрерывной на отрезке функции 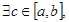такая, что 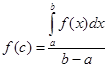или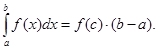
Замечание
Это свойство обычно называют теоремой о среднем.

Date: 2015-09-05; view: 541; Нарушение авторских прав