Касательная и нормаль к плоской кривой

Пусть даны кривая y = f(x) и точка M (x1; y1) на ней. Требуется составить уравнения касательной и нормали (смотри рисунок).

Как известно, угловой коэффициент k касательной к кривой y = f(x) в точке M (x1; y1) равен значению f '(x1) производной y' = f '(x) при x = x1/ Следовательно, уравнение касательной можно записать в виде уравнения прямой, проходящей через данную точку в данном направлении, т.е. в виде y - y1 = f '(x1)(x - x1)

Нормалью называется прямая, проходящая через точку касания перпендикулярно касательной. поэтому ее угловой коэффициент равен 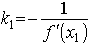, а уравнение записывается в виде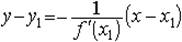

Ф-ии нескольких переменных. Основные понятия (область определения, предел,, непрерывность)

Определение 4.1. Если каждой точке M(x1,x2,...,xn) некоторой области D из пространства Rⁿ соответствует вполне определенное число z ∈ R, то говорят, что задана функция n переменных z=f(x1,x2... xn) (z=f (M)). обозначается D (f).

Множество D называется областью определения функции и обозначается D (f).Обычно под областью определения аналитически заданной функции подразумевается ее естественная область определения.

Множество E (f) = { z ∈ R z = f (M), M ∈ D (f)} называется областью значений функции f. Если n = 2, то функция z = f (M) переходит в функцию двух независимых переменных z = f (x, y), где (x, y)∈ D ⊂ R ².

Определение 4.4. Говорят, что последовательность точек M1(x1,y1), M2 (x2,y2)…Mn (xn, yn) плоскости x 0 y сходится к точкеM0(x0,y0), если расстояние dn= 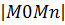= 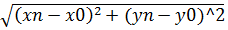стремится к нулю когда n →∞.

Определение 4.5. Число A называется пределом функции f (x, y) в точке M0, если для любой последовательности точек M1,M2,Mn…. сходящейся к точке M0, соответствующая последовательность значений функции f(M1), f(M2)….f(Mn) сходится к числу А: lim _{M → M0} f(M)

Определение 4.7. Функция z = f (x, y) называется непрерывной в точке M0(x0,y0), если она определена в самой точке M0 и некоторой ее окрестности и выполняется равенство lim _{M → M0} f(M)=f(M0) т.е. предел функции в точке равен значению функции в этой точке.

Определение 4.8. Функция z = f (x, y) называется непрерывной в области R, если она непрерывна в каждой точке этой области.

Date: 2015-09-05; view: 482; Нарушение авторских прав