Частные производные и полный дифференциал

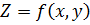опред в окрестности точки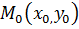

Частной производной (1-го порядка) ф-ции нескольких переменных по одной из этих переменных наз предел отношения соответствующего частного приращения ф-ции к приращению данной переменной, когда последнее стремится к нулю.

Пусть 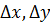– приращения независимых переменных x и y в некоторой точке 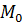из области X. Тогда величина, равная 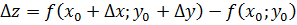наз полным приращением ф-ции в точке 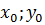. Если переменную х зафиксировать, а переменно у дать приращение 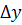, то получим 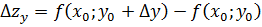. Аналогично определяется частная производная от переменной у.

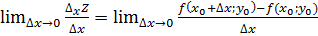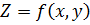Частная производная по х: . Аналогично опред ч произ от y: . Част произв ф-ции по переем х обазнач: 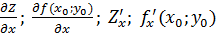. Аналогично для y.

Правило вычисл-я ч произв: Т.к. при вычисл ч произв по перем х знач-е перем y счит фиксир, то отнош 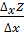явл ф-ей завис от х.

Т.о. вычисл-е ч произв по х сводится к вычисл произв ф-ции 1 переменной, завис от х, при этом y=const

Для функции 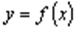одной переменной производная n –го порядка определялась следующим образом: 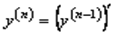. Аналогично определяются и частные производные высших порядков.

Частной производной n–го порядка функции нескольких переменных называется частная производная первого порядка от частной производной (n –1–го порядка той же функции.

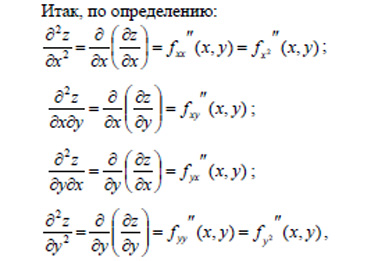
Частная производная 2–го или более высокого порядка, взятая по нескольким различным переменным, называется смешенной частной производной.

Справедлива теорема:

Две смешанные частные производные одной и той же функции, отличающиеся лишь порядком дифференцирования, равны между собой при условии их непрерывности.

Так,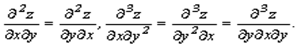

Полный дифференциал и его примене­ние в приближенных вычислениях.

Полное приращ ф-ции 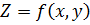опред в окрестности точки 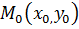– разность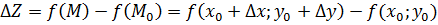

Если полное приращ ф-ции 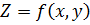в т 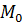представимо в виде 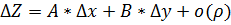(1), то ф-я наз дифференцируемой ф-ей в т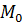

Гл часть 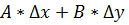– дифференциал ф-ции в данной точке

В ф-ле (1) A и B – const, 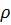– расстояние между точками M и M₀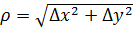 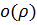– бесконечно малое более высокого порядка чем .

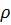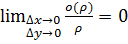
Дифференциал ф-ции: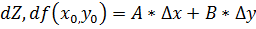

Теорема. Дифференциал ф-ции 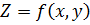в т 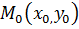вычисл след обр

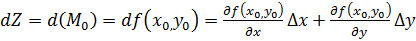. Если ввести обознач 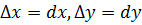, то 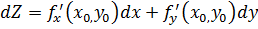(2) Ф-ла (2) опред дифференциал в заданной точке

Док-во:Пусть 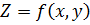диференцируема в точке 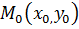. Тогда полное приращ 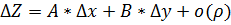. Положим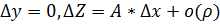

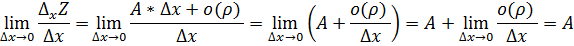
Из этого следует, что A= 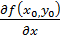. Аналогичным образом доказывается, что B в ф-ле дифференциала (2)=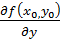

9. Экстремум ф-ии нескольких переменных. Необходимые и достаточные условия экстремума

Пусть функция 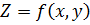определена в некоторой области D и точка .

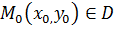Функция 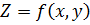имеет в точке 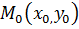локальный максимум, если существует такая окрестность этой точки, что для всех точек M (x, y) этой окрестности выполняется неравенство .

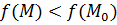Функция 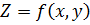имеет в точке 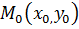локальный минимум, если существует такая окрестность этой точки, что для всех точек M (x, y) этой окрестности выполняется неравенство .

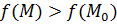Максимум и минимум функции называются экстремумами функции.

Необходимые и достаточные ус­ловия.

Теорема (необходимое условие экстремума). Если ф-я 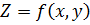диференцируема в окрестности точки 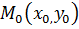и в этой точке сущ экстремум ф-ции, то частные произв ф-ции по обоим переменным в этой точке =0.

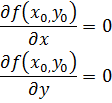
Замечание 1. Если ф-я u = f(x, y, z), то необход условием сущ экстремума ф-ции в точке 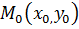явл рав-во нулю всех ее частных производных в этой точке.

Таким обр первый этап нахождения экстремума ф-ции сост в нахожд стацион точек.

Не дифференцир ф-я может принимать экстремальные значения в точках, в к-х производная не сущ.

Теорема (достаточное условие экстремума).

Пусть функция 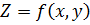определена в некоторой окрестности точки 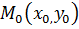и имеет в этой окрестности непрерывные частные производные до второго порядка включительно. Если выполняются условия:

1) частные производные первого порядка в точке 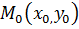равны нулю: ..

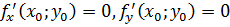2) для чисел выполняется неравенство:

а) 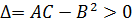, то в точке функция имеет экстремум, причем минимум, если A>0 и максимум, если A<0

б) 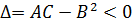, то в этой точке экстремума нет.

Если Δ=0, то нужны дополнительные исследования.