Задача 4.7 (25)

Со стержня ОА (рис. 4.21), вращающегося с постоянной угловой скоростью w вокруг вертикальной оси z, слетает колечко M. В условиях пренебрежимо малого трения движение колечка по стержню описывается законом

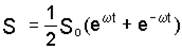, (а)

где S₀ – расстояние от оси вращения до колечка в начальный момент. Положительное направление отсчета расстояний показано на рис. 4.21 стрелкой 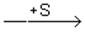; e – основание натурального логарифма.

Определить абсолютное ускорение колечка.

Решение

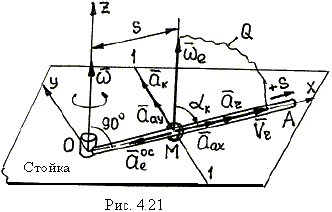
1. Расчетная схема с указанием колечка М, совершающего сложное движение, изображена на рис. 4.21. 2. Анализ движения: движение колечка М по отношению к стойке (абсолютное движение) складывается из движения колечка вдоль стержня ОА и движения вместе со стержнем.

Первое из складываемых движений является относительным, второе – переносным.

3. Запишем векторное уравнение (4.2):

` а<sub>а</sub> =` а_е +` а<sub>r</sub> +` а_k. (б)

Установим формулы для определения ускорений, входящих в уравнение (б), и выполним предварительные вычисления.

Абсолютное ускорение` а<sub>а</sub>. Напомним, что вид формулы` а_а зависит от формы траектории абсолютного движения точки. Эта траектория в рассматриваемом примере – плоская кривая, форма которой не задается. Поэтому вектор` а_а представляем в соответствии с (4.5) составляющими по направлению осей х и у (см. рис. 4.21)

` а<sub>а</sub> =` а_ах +` а_ау.

Переносное ускорение` а<sub>е</sub>. Напомним, что вид формулы` а_е определяется характером переносного движения. В данной задаче переносным движением является вращение стержня ОА вокруг оси z. Поэтому вектор` а_е представим в соответствии с (4.7) в виде

,

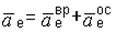где ; ;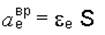

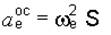S – расстояние от точки M до оси вращения z [см. формулу (а)];
w _e – переносная угловая скорость, равная заданной угловой скорости стержня ОА,` w <sub>e</sub> =` w _ОА =` w; вектор` w направлен по оси вращения z в сторону, определяемую правилом правого винта (рис. 4.21); e _e – переносное угловое ускорение, равное в данном случае нулю, так как по условию задачи w = const.

В результате

, .

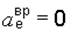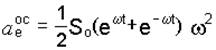Вектор 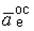направлен по радиусу к оси вращения z. Так как 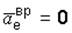, то окончательно будем иметь

.

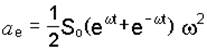Относительное ускорение` а<sub>r</sub>. Напомним, что вид формулы` а_r определяется характером траектории относительного движения. В данной задаче эта траектория – прямая линия ОА. Поэтому по формуле (4.8) имеем:

.

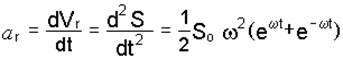Производная 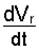получилась со знаком “плюс”, поэтому вектор` а_r направляется по прямой ОА в сторону положительного отсчета координаты S, т.е. от M к А. Отметим, что а_r = a_e для любого момента времени.

Ускорение Кориолиса` а<sub>k</sub>. Модуль и направление вектора` а_k выражается формулой (4.12):

.

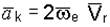Вектор` w _e направлен по оси z, его модуль задан условием задачи. Относительная скорость V_r определяется по формуле

.

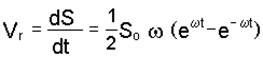Производная 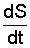получилась со знаком “плюс”, поэтому вектор ` V_r направляется по прямой ОА в сторону положительного отсчета координаты S, т.е. от М к А.

Перенесем векторы` w <sub>e</sub> и` V_r в точку М.

Определим по правилу векторного произведения направление ускорения` а<sub>k</sub>. Для этого сначала проведем через векторы` w _e и` V<sub>r</sub> плоскость Q (см. рис. 4.21). Затем проведем прямую 1–1, перпендикулярную плоскости Q. Наконец, направим по прямой 1–1 вектор` а_k в ту сторону, откуда вращение вектора` w <sub>e</sub> к` V_r видно происходящим против часовой стрелки (см. рис. 4.21).

Определим модуль ускорения ` а_k по формуле (4.13):

,

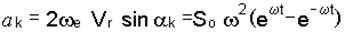так как здесь угол a = 90°.

4. В результате проведенного анализа и предварительных вычислений имеем в уравнении (б) две неизвестные величины: а_ах и а_ау. Из анализа следует, что все векторы, входящие в уравнение (б), лежат в одной плоскости. Это позволяет перейти к проектированию векторного уравнения на оси координат, но сначала приведем уравнение (б) к виду (4.14), учитывая предварительные вычисления

.

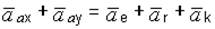Спроектируем это уравнение на оси выбранной системы координат:

(х) 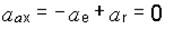, так как 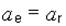(см. выше);

(у) .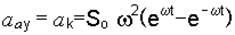

Модуль абсолютного ускорения колечка М равен:

.

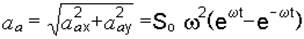Отметим, что абсолютное ускорение колечка получилось равным кориолисову ускорению. Легко убедиться, что это будет при любом положении колечка на стержне.

Date: 2015-09-18; view: 528; Нарушение авторских прав