Определение ускорений в сложном движении точки

Зависимость между ускорениями определяется теоремой Кориолиса: абсолютное ускорение` а<sub>а</sub> точки равно геометрической сумме переносного` а _е, относительного` а <sub>r</sub> и кориолисова` а _k ускорений, т.е.

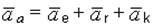. (4.2)

Прежде чем приступить к решению этого уравнения в конкретной задаче, надо установить по каким формулам определяются` а<sub>а</sub>,` а _e, ` а <sub>r</sub>, ` а _k.

Абсолютное ускорение` а<sub>а</sub>. Напомним определение (см. подразд. 4.1): абсолютным ускорением точки называется ее ускорение в движении относительно неподвижного тела. Вид формулы` а_а зависит от формы траектории абсолютного движения точки.

Если траектория – прямая линия, то

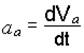. (4.3)

Ускорение` а<sub>а</sub> в этом случае совпадает с траекторией точки. Направление вектора` а_а по траектории точки определяется знаком производной (4.3): при знаке “плюс” направлено в сторону положительного отсчета расстояний на траектории, при знаке “минус” – в противоположную сторону.

Если траектория абсолютного движения – окружность, то

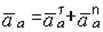, (4.4)

где 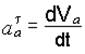– касательное абсолютное ускорение; 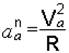– нормальное абсолютное ускорение; R – радиус окружности.

Направление вектора 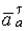по касательной устанавливается с учетом знака производной 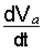[см. пояснения к формуле (4.3)]. Вектор 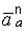всегда направляется по радиусу окружности к ее центру.

Если траектория абсолютного движения не задается, то абсолютное ускорение следует разложить на составляющие по направлениям осей прямоугольной системы координат Охуz:

для плоских кривых

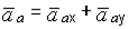; (4.5)

для пространственных кривых

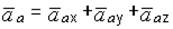. (4.6)

Переносное ускорение` а _е. Напомним определение (см. подразд. 4.1): переносным ускорением называется ускорение точки перемещающегося тела, с которой совпадает в данный момент движущаяся по этому телу точка.

Вид формулы` а _е определяется характером переносного движения.

Если переносное движение тела – поступательное, то в качестве` а _е можно взять ускорение любой точки этого тела. (Напомним, что все точки тела при поступательном движении имеют одинаковые ускорения).

Если переносное движение тела – вращение вокруг неподвижной оси, то

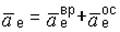, (4.7)

где 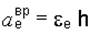– вращательное переносное ускорение; 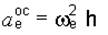– осестремительное переносное ускорение.

В этих формулах w _е и e _е – угловая скорость и угловое ускорение тела; h – расстояние от точки М до оси вращения или радиус вращения точки.

Вектор 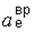направлен перпендикулярно радиусу вращения в сторону дуговой стрелки углового ускорения e _е. Вектор 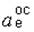направлен по радиусу к оси вращения.

Если переносным движением будет плоскопараллельное или какое-либо более сложное движение тела, то формулы для определения а _е следует взять из соответствующего раздела кинематики твердого тела.

Относительное ускорение` а _r. Напомним определение (см. подразд. 4.1): относительным ускорением точки называется ее ускорение в движении относительно перемещающегося тела.

Вид формулы` а _r определяется характером траектории относительного движения.

Если траектория – прямая линия, то

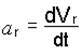. (4.8)

Ускорение` а <sub>r</sub> в этом случае совпадает с траекторией точки. Направление вектора` а _r по траектории определяется знаком производной (4.8): при знаке “плюс”` а _r направлено в сторону положительного отсчета расстояний на траектории, при знаке “минус” – в противоположную сторону.

Если траектория относительного движения – окружность, то

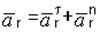, (4.9)

где 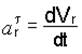– касательное относительное ускорение; 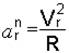– нормальное относительное ускорение; R – радиус окружности.

Направление вектора 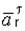по касательной устанавливается с учетом знака 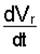[см. пояснения к формуле (4.8)]. Вектор 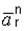направляется по радиусу окружности к ее центру.

Если траектория относительного движения не задается, то относительное ускорение следует разложить на составляющие по направлению осей прямоугольной системы координат Oxyz:

для плоских кривых

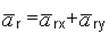; (4.10)

для пространственных кривых

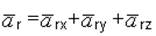. (4.11)

Ускорение Кориолиса выражается формулой

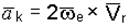. (4.12)

Чтобы определить модуль и направление` а _k, нужно выполнить следующие операции:

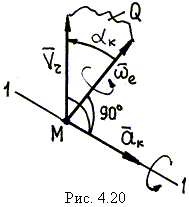
– отложить от точки M (рис. 4.20) вектор переносной угловой скорости` w e и вектор относительной скорости точки` Vr. (Напомним, что вектор` w e направляется по оси вращения в сторону, определяемую правилом правого винта);

– определить по правилу векторного произведения (4.12) направление ускорения` а <sub>k</sub>: для этого надо провести через векторы` w _e и` V<sub>r</sub> плоскость Q; затем провести прямую 1-1, перпендикулярную плоскости Q; наконец, направить по прямой 1–1 вектор` а _k в ту сторону, откуда вращение вектора` w <sub>e</sub> к` V_r видно происходящим против хода часовой стрелки (см. рис. 4.20);

– определить модуль ускорения` а _k как модуль векторного произведения (4.12):

, (4.13)

где а _k – угол между векторами` w <sub>e</sub> и` V_r.

Если переносное движение поступательное, то` w <sub>e</sub> = 0, следовательно,` а _k равно нулю. Ускорение Кориолиса равно нулю также, если векторы` w <sub>e</sub> и` V_r параллельны, или когда один из этих векторов обращается в нуль в рассматриваемый момент времени.

После того, как вид формул определения` а<sub>а</sub>,` а _е,` а <sub>r</sub> и` а _k установлен, рекомендуется переписать уравнение (4.2) с учетом того, что некоторые члены уравнения будут представлены составляющими.

Допустим, по условию задачи траектория абсолютного движения – окружность, переносное движение – вращение тела вокруг оси, а траектория относительного движения – прямая линия; в этом случае уравнение (4.2) с учетом (4.4), (4.7), (4.8) примет вид

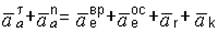. (4.14)

В других задачах число слагаемых в левой и правой частях уравнения (4.14), конечно, может быть иным.

Для решения уравнения типа (4.14) оно проектируется на оси подвижной или неподвижной системы координат. Если все векторы этого уравнения лежат в одной плоскости, то будем иметь два уравнения проекций, для пространственной задачи – три уравнения проекций.

Отсюда следует, что в плоских задачах уравнение (4.14) будет разрешимо, если в нем содержится не более двух, а в пространственных – не более трех неизвестных величин.

В качестве неизвестных могут быть любые величины, входящие в выражения абсолютного, переносного, относительного и Кориолисова ускорений или же сами эти ускорения.

Значит, решению уравнения типа (4.14) должно предшествовать предварительное определение части величин, входящих в выражения` а<sub>а</sub>,` а _е,` а <sub>r</sub> и` а _k. Они определяются из условия задачи по известным соотношениям кинематики точки и тела; во многих случаях используются результаты определения скоростей в данной задаче.

Как обобщение всего вышесказанного, предлагается такая последовательность операций при решении задачи в сложном движении точки.

1. Нарисовать по условию задачи расчетную схему, на которой отметить точку М, совершающую сложное движение.

2. Указать относительное, переносное и абсолютное движение точки в соответствии с рекомендациями подразд. 4.1.

3. Записать векторное уравнение (4.2) и провести его анализ: установить формулы для определения` а<sub>а</sub>,` а _е,` а <sub>r</sub> и` а _k [см. формулы (4.3)... (4.13)]; преобразовать уравнение (4.2) в уравнение типа (4.14); выполнить предварительные вычисления так, чтобы в уравнении типа (4.14) осталось не более двух неизвестных величин в плоских задачах, и не более трех – в пространственных задачах; отложить все указанные ускорения или их составляющие от точки М на расчетной схеме.

4. Спроектировать уравнение типа (4.14) на оси выбранной системы координат. Из получившихся алгебраических уравнений проекций определить оставшиеся неизвестные величины.

Date: 2015-09-18; view: 744; Нарушение авторских прав