
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача 3.13 (17)
|
|
Груз В, опускаясь, приводит в движение катушку с помощью нити, переброшенной через блок С. Считая, что катушка катится без скольжения, определить ускорение точки А, если в данный момент VВ = 80 см/с, а В = 160 см/с2. Радиусы катушки r = 30 см; R = 50 см.
Решение
1. Рассматриваемый механизм (рис. 3.35) состоит из груза В, совершающего поступательное движение, и катушки, совершающей плоскопараллельное движение.
- Решение задачи определения скоростей. Скорость точки К касания нити с катушкой равна скорости груза, т.е. VК = VВ. Мгновенный центр скоростей катушки находится в точке Р (рис. 3.36).
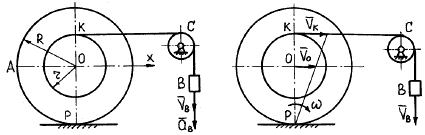
Рис. 3.35 Рис. 3.36
Угловая скорость катушки
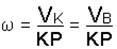 . (д)
. (д)
В данному случае w = 1 1/с.
Скорость центра О катушки
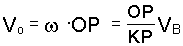 . (е)
. (е)
В данном случае VО = 50 см/с.
3. Ведущим звеном механизма является груз В, ускорение которого задано условием задачи.
Ведущее звено и катушка связаны гибкой нитью. Точка К нити имеет, очевидно, такое же по модулю ускорение, как и груз В.
4. Решение задачи об определении ускорений точек катушки, совершающей плоскопараллельное движение. Выберем в качестве полюса центр катушки. Так как центр катушки движется прямолинейно по оси х (рис. 3.35), его ускорение направлено по этой же оси, а модуль определится дифференцированием уравнения (е)
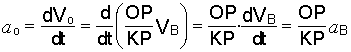 ,
,
 см/с2.
см/с2.
Такое дифференцирование возможно, потому что при качении катушки без проскальзывания расстояния ОР и КР остаются неизменными.
Составим векторное уравнение типа (3.10) для точки А
 . (ж)
. (ж)
Изобразим все векторы, входящие в уравнение (ж) на рис. 3.37.
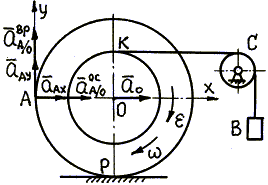 Рис. 3.37.
Рис. 3.37.
| Неизвестное по направлению ускорение точки А представим составляющими` а Aх и` а Aу. Осестремительную составляющую 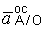 направим от точки А к полюсу О, вращательную составляющую направим от точки А к полюсу О, вращательную составляющую 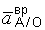 направим перпендикулярно направим перпендикулярно 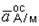 вверх, потому что катушка катится ускоренно (см. задачу 3.10). вверх, потому что катушка катится ускоренно (см. задачу 3.10).
|
Приступим к анализу векторного уравнения (ж). Задача об определении ускорений при качении катушки без проскальзывания относится к типу 2. Неизвестными векторного уравнения (ж) являются составляющие` а Ах и` а Ау. Ускорение полюса О определено выше. После определения угловой скорости (см. с. 53) легко вычисляется величина осестремительной составляющей 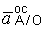 :
:
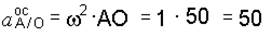 см/с2.
см/с2.
Учитывая, что расстояние КР в формуле (д) остается постоянным, угловое ускорение колеса найдем дифференцированием:
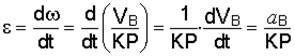 .
.
В данном случае 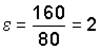 1/с2.
1/с2.
Величина вращательной составляющей 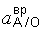 равна
равна
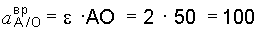 см/с2.
см/с2.
Проектируя векторное уравнение (ж) на оси координат, получим:
(х) 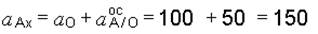 см/с2,
см/с2,
(у) 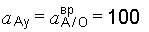 см/с2.
см/с2.
Полное ускорение точки А:
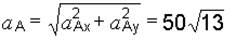 см/с2.
см/с2.
Date: 2015-09-18; view: 737; Нарушение авторских прав