Определение скоростей в сложном движении точки

Напомним установленные в подразд. 4.1 определения и обозначения:

• относительной скоростью точки называется ее скорость в движении относительно перемещающегося тела, обозначение –` V<sub>r</sub>;
• переносной скоростью называется скорость точки перемещающегося тела, с которой в данный момент совпадает движущаяся по телу точка (см. рис. 4.2), обозначение –` V_е;
• абсолютной скоростью точки называется ее скорость в движении относительно неподвижного тела, обозначение –` V _а.

Зависимость между скоростями определяется теоремой:
абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей, т.е.

` V <sub>а</sub> = ` V_е +` V_r. (4.1)

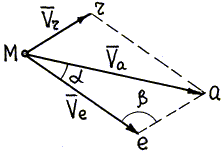Рис. 4.11.

Из уравнения (4.1) следует, что абсолютная скорость есть диагональ параллелограмма, построенного на переносной и относительной скоростях. Если параллелограмм Ме а r (рис. 4.11) построить в масштабе, то тем самым задача по определению` V а будет решена: модуль абсолютной скорости равен длине диагонали М а в принятом масштабе, а направление абсолютной скорости – от М к а.

Но при решении задач кинематики параллелограмм скоростей Ме а r обычно рассматривается как вспомогательный чертеж, а модуль и направление искомой скорости определяется аналитически с использованием известных из геометрии соотношений между элементами треугольника (имеется в виду теорема косинусов и т.д.), иначе говоря, задача сводится к решению треугольника Me a r. При этом искомой величиной может быть не только V _a, а любой из пяти элементов треугольника – V _a, V_e, V_r, a, b.

Задача будет разрешимой, если из пяти указанных элементов неизвестными будут два, например, V _a и a, V_е и V_r. Это значит, перед тем, как решать треугольник, надо по условию задачи определить, по крайней мере, три элемента треугольника. Эти три элемента или три кинематические характеристики будем в дальнейшем называть предварительно определяемыми.

Во многих случаях предварительно определяемые величины легко отождествляются с величинами, заданными условием задачи. В остальных случаях их можно найти по данным задачи с использованием формул “Кинематики точки” или “Кинематики твердого тела” (см. разд. 1, 2, 3 данного пособия).

При решении задач определенную сложность для начинающих представляет правильное построение параллелограмма скоростей по уравнению (4.1). Рекомендуется делать это в следующем порядке.

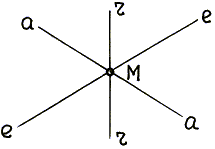Рис. 4.12.

Вначале на расчетной схеме надо провести три линии, по которым должны быть направлены` V а,` Vе и` Vr. Эти линии будем обозначать соответственно а – а, е–е, r–r (рис. 4.12); они должны проходить через точку М, которая по условию задачи совершает сложное движение.

Линия а – а проводится по касательной к траектории абсолютного движения; линия r–r – по касательной к траектории относительного движения; линия e–e – проводится в соответствии с правилами, установленными для соответствующего движения тела.

Если положение какой-либо линии скорости установить по условию задачи нельзя, то ее следует провести под некоторым углом a к уже проведенной линии скорости, считая в дальнейшем a искомой величиной.

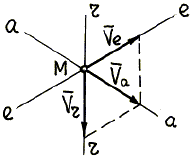Рис.4.13.

Далее на расчетной схеме надо изобразить в произвольном масштабе скорость, направление которой задано условием задачи; ее надо отложить от точки М по соответствующей линии; построить параллелограмм скоростей, следя за тем, чтобы` V а была диагональю этого параллелограмма (рис. 4.13).

Как обобщение вышесказанного, предлагается такая последовательность операций при решении задачи скоростей в сложном движении точки.

1. По условию задачи нарисовать расчетную схему, на которой отметить точку М, совершающую сложное движение.

2. Указать относительное, переносное и абсолютное движение в соответствии с рекомендациями подразд. 4.1.

3. Провести через точку М линии скоростей а – а, е–е, r–r в соответствии с пояснениями к рис. 4.12.

4. Отложить от точки М заданную скорость по соответствующей линии, а затем построить параллелограмм скоростей (рис. 4.13).

5. Найти по условию задачи три предварительно определяемые величины.

6. Решая треугольник Ме а (рис. 4.11 или 4.13), найти оставшиеся искомые

Date: 2015-09-18; view: 949; Нарушение авторских прав