Задача 4.1

Вдоль цеха по рельсам с постоянной скоростью 0,1 м/с перемещается мостовой кран АВ, по которому с постоянной скоростью 0,2 м/с движется тележка М. Определить абсолютную скорость тележки.

Решение

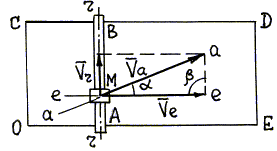Рис. 4.14.

1. На расчетной схеме (рис. 4.14) изображена точка М (тележка), совершающая сложное движение и подвижное тело – кран АВ в заданный момент времени. 2. Результаты анализа сложного движения тележки (пример 1):

• относительное движение – движение тележки М по крану АВ;
• переносное движение – движение крана АВ относительно цеха ОСDE;
• абсолютное движение – движение тележки М относительно цеха.

3. Проводим через точку М линии скоростей. Траектория относительного движения точки М – прямая АВ, поэтому линия r–r совпадает с АВ; переносным движением является поступательное движение крана вдоль стороны ОЕ цеха, поэтому линия e–e проведена параллельно OE; траекторию абсолютного движения точки М установить по условию задачи нельзя, поэтому линию а–а проводим под некоторым углом a к линии е–е, считая a искомой величиной.

4. Построим параллелограмм скоростей: по условию задачи известны направления относительной скорости точки (она равна скорости движения тележки по крану) и переносной скорости (она равна скорости точки крана, с которой в данный момент совпадает тележка); откладываем от точки М по линии r–r вектор относительной скорости` V<sub>r</sub>, а по линии е–е – вектор переносной скорости ` V_е; затем достраиваем параллелограмм скоростей.

5. По условию задачи имеем V_r = 0,2 м/с, V_е = 0,1 м/с, угол b = 90°.

6. Решая треугольник Меа (рис. 4.14), находим

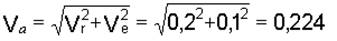м/с;

.

Задача 4.2

По трубке, изогнутой в форме окружности радиуса R = 20 см (рис. 4.15), течет жидкость с постоянной относительно трубки скоростью 40 см/с. Трубка вращается вокруг оси О с постоянной угловой скоростью w = 1 1/с. Найти абсолютную скорость частицы жидкости, когда она занимает в трубке положение, определяемое углом ОСМ, равным 120°. Направления вращения трубки и течения жидкости (по трубке) – против хода стрелки часов.

Решение

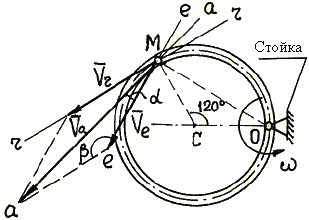Рис. 4.15.

1. Расчетная схема с указанием частицы М жидкости в заданном положении изображена на рис. 4.15. 2. Результаты анализа сложного движения частицы М (пример 2): относительное движение – движение частицы М по трубке; переносное движение – вращение трубки вокруг оси О стойки; абсолютное движение – движение частицы М относительно стойки.

3. Проводим через точку М линии скоростей: траектория относительного движения точки М – окружность с центром в точке С, поэтому линия r–r проведена по касательной к этой окружности; переносным движением здесь является вращение трубки вокруг оси О, поэтому линия е–е проведена перпендикулярно ОМ, т.е. по направлению скорости точки М' трубки; траекторию абсолютного движения точки М здесь, как и в задаче 4.1, заранее установить нельзя, поэтому линию а–а проводим под углом a к линии е–е, считая a искомой величиной.

4. Построение параллелограмма скоростей: по условию задачи известны направления` V<sub>r</sub> (` V_r – скорость движения по трубке) и` V<sub>е</sub> (` V_е – скорость точки М' трубки), откладываем от точки М векторы ` V<sub>r</sub> и` V_е по линиям r–r и e–e; затем достраиваем параллелограмм скоростей.

5. Предварительные вычисления: по условию задачи имеем V_r = 40 см/с, модуль переносной скорости определяем по формуле

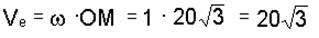см/с,

из схемы на рис. 4.15 следует, что b = 150°.

6. Решая треугольник Mea, находим

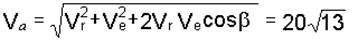см/с;

.

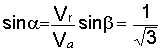Задача 4.3

На неподвижную проволочную окружность радиуса20 см надето колечко М (рис. 4.16); через него проходит стержень ОА, который вращается вокруг оси О против часовой стрелки с угловой скоростью w = 1 1/с. Найти относительную, переносную и абсолютную скорости колечка М в момент, когда угол ОСМ равен 90°.

Решение

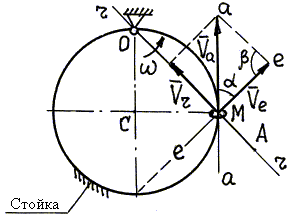Рис. 4.16.

1. Расчетная схема с указанием колечка М в заданном положении (угол ОСМ равен 90°) изображена на рис. 4.16. 2. Результаты анализа сложного движения колечка М (пример 3): относительное движение – движение колечка М по стержню ОА; переносное движение – вращение стержня ОА вокруг оси О стойки; абсолютное движение – движение колечка М относительно стойки по окружности радиуса СМ.

3. Проводим через точку М линии скоростей: линия r–r проведена вдоль ОА – траектории относительного движения; линия е–е проведена перпендикулярно ОА, – так направлена скорость точки М' стержня ОА (переносная скорость` V_e); траектория абсолютного движения колечка М – окружность с центром в точке С, поэтому линия а–а проведена по касательной к этой окружности.

4. Построение параллелограмма скоростей: по условию задачи известно направление` V<sub>e</sub> (` V_e – скорость точки М' стержня ОА), откладываем ее от точки М по линии е–е; далее достраиваем параллелограмм скоростей, чтобы` V_а была диагональю.

5. Предварительные вычисления: по условию задачи определяем

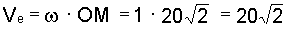см/с;

из схемы на рис. 4.16 следует, что a = 45°, b = 90°.

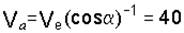6. Решая треугольник Меа, находим см/с,

см/с.

Задача 4.4

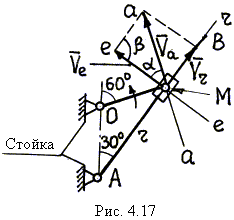
В кулисном механизме (рис. 4.17) при вращении кривошипа ОМ вокруг оси О ползун М, перемещаясь вдоль стержня АВ, приводит этот стержень во вращательное движение вокруг оси А. Для положения механизма, изображенного на рисунке, определить скорость перемещения ползуна М по стержню АВ и угловую скорость стержня АВ, если угловая скорость кривошипа ОМ w ОМ = 2 1/с, длина кривошипа ОМ равна 10 см. Кривошип вращается против часовой стрелки.

Решение

1. Расчетная схема механизма изображена на рис. 4.17.

2. Результаты анализа сложного движения ползуна М (пример 4):

• относительное движение – движение ползуна М по стержню АВ;
• переносное движение – вращение стержня АВ вокруг оси А стойки;
• абсолютное движение – движение ползуна М относительно стойки по окружности радиуса ОМ.

3. Проводим через точку М линии скоростей: линия r–r проведена вдоль АВ, т.е. по траектории относительного движения ползуна М; линия е–е проведена перпендикулярно АВ – так направлена скорость точки М' стержня АВ (или переносная скорость); линия а–а проведена перпендикулярно ОМ, что соответствует направлению касательной к окружности радиуса ОМ – траектории абсолютного движения ползуна М.

4. Построение параллелограмма скоростей: по условию задачи известно направление` V<sub>а</sub>, откладываем ее от точки М по линии а–а. Далее достраиваем параллелограмм скоростей, в котором` V_а – диагональ.

5. Предварительные вычисления: по условию задачи определяем

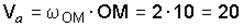см/с;

из схемы на рис. 4.17 следует a = 30°, b = 90°.

6. Решая треугольник Меа, находим

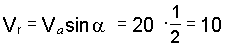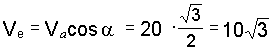см/с;

см/с.

После этого определяем угловую скорость стержня АВ

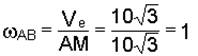1/с.

Задача 4.5

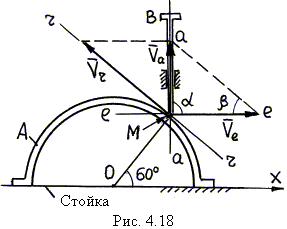
Кулачок А (рис. 4.18), перемещаясь по горизонтальной плоскости вдоль оси х, приводит в движение толкатель ВМ, скользящий в вертикальных направляющих. Определить скорость толкателя в вертикальных направляющих в положении механизма, изображенного на рис. 4.18, если в этот момент скорость кулачка равна 30 см/с.

Решение

1. Расчетная схема изображена на рис. 4.18.

2. Результаты анализа сложного движения точки М (см. пример 5):

• относительное движение – движение точки М по поверхности кулачка А;
• переносное движение – движение кулачка А относительно стойки;
• абсолютное движение – движение точки М относительно стойки по вертикали.

3. Проводим через точку М линии скоростей: линия r–r проведена по касательной к поверхности кулачка или иначе – по касательной к траектории относительного движения; линия e–e проведена параллельно оси х – так направлена скорость точки кулачка, с которой в данный момент совпадает конец М толкателя ВМ (или переносная скорость` V_е); линия а–а проведена по вертикали – по траектории абсолютного движения.

4. Построение параллелограмма скоростей: по условию задачи известно направление` V<sub>е</sub>, откладываем ее от точки М по линии е–е; далее достраиваем параллелограмм скоростей, в котором` V_а – диагональ.

5. По условию задачи имеем V_е = 30 см/с. Из схемы на рис. 4.18 следует, что a = 90°, b = 30°.

6. Решая треугольник Меа, находим искомую скорость толкателя

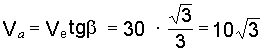см/с.

Задача 4.6

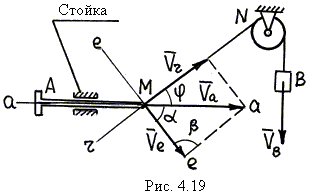
В механизме на рис. 4.19 определить зависимость между скоростью штока АМ и скоростью опускания груза В (угол j задан). Решение 1. Расчетная схема изображена на рис. 4.19. 2. Результаты анализа сложного движения точки М (см. пример 6):

• относительное движение – движение точки М вдоль троса МN;
• переносное движение – вращение троса MN вокруг точки N;
• абсолютное движение – движение точки М относительно стойки по горизонтали.

3. Проводим через точку М линии скоростей; линии а–а и r–r совпадают с прямолинейными траекториями абсолютного и относительного движений; линия е–е проведена перпендикулярно MN – так направлена скорость точки M' троса в переносном вращательном движении вокруг N.

4. Построение параллелограмма скоростей: по условию задачи известно направление скорости` V<sub>В</sub> (вниз), для точки М это соответствует заданию` V_r; откладываем` V<sub>r</sub> по линии r–r, а затем достраиваем параллелограмм скоростей, в котором` V_a – диагональ.

5. Из схемы на рис. 4.19 следует, что a = 90° – j, b = 90°.

6. Решая треугольник Меа, находим

.

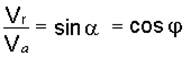Учитывая, что V_r = V_B, V_a = V_АМ, получим

.

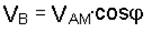Date: 2015-09-18; view: 866; Нарушение авторских прав