Задача 3.14 (18)

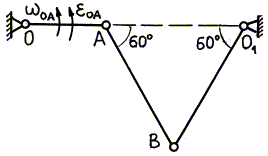Рис. 3.38.

Кривошип ОА шарнирного четырехзвенника ОАВО1 (рис. 3.38) имеет в данный момент времени угловую скорость w ОА = 2 1/с и угловое ускорение 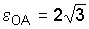1/с2, ОА = 10 см, АВ = ВО1 = 20 см. Для данного положения механизма определить ускорение точек В и С, а также угловые ускорения звеньев АВ и ВО1; АС = СВ.

Решение

1. В рассматриваемом механизме звенья ОА и ВО₁ совершают вращательное движение, а звено АВ – плоскопараллельное движение.

2. Решение задачи определения скоростей. Найдем скорость точки А ведущего звена ОА:

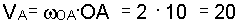см/с.

Для звена АВ вначале найдем мгновенный центр скоростей. Так как` V<sub>A</sub> ^ OA, а` V_В ^ ВO₁, то МЦС должен лежать на пересечении прямых, проведенных через ОА и ВО₁. Это значит, что МЦС звена АВ в заданном положении механизма совпадает с центром шарнира О₁ (рис. 3.39).

Тогда 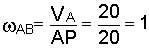1/с.

Скорость точки В 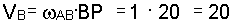см/с.

Зная скорость точки В, найдем

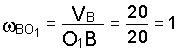1/с.

3. Решение задачи об определении ускорения точки А ведущего звена – кривошипа ОА. При вращательном движении кривошипа ускорение точки А имеет две составляющие – осестремительную и вращательную (рис. 3.40)

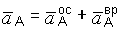, (з)

где

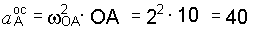см/с²;

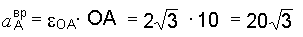см/с².

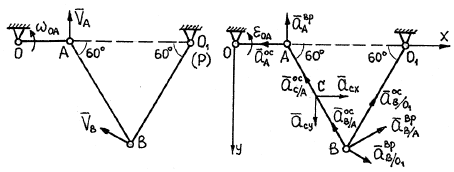
Рис. 3.39 Рис. 3.40

4. Решение задачи об определении ускорений точки В звена АВ, совершающего плоскопараллельное движение.

Звено АВ связано с ведущим кривошипом ОА шарниром А. Выберем точку А за полюс.

Составим векторное уравнение типа (3.10) для точки В

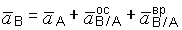
или с учетом (з)

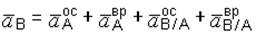. (и)

Покажем все векторы, входящие в уравнение (и), на рис. 3.40.

Ускорение точки В представим двумя составляющим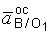и и 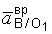, так как точка В принадлежит не только стержню АВ, но и вращающемуся стержню ВО₁, т.е.

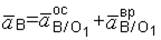. (к)

Вектор 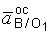направлен от точки В к оси вращения О₁, вектор 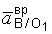направлен перпендикулярно ВО₁.

Осестремительное ускорение точки В при вращении стержня АВ вокруг полюса А 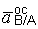направлено от точки В к полюсу А, вращательное ускорение 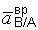– перпендикулярно АВ.

С учетом выражения (к) векторное уравнение (и) примет вид

. (л)

Приступим к анализу этого уравнения. Модуль осестремительной составляющей 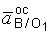легко определяется

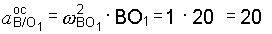см/с².

Модуль вращательной составляющей 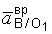найти до решения векторного уравнения (л) нельзя, так как в выражении

угловое ускорение e _ВО1 – величина неизвестная. Дифференцирование выражения 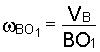не дает результата, так как закон изменения V_В нам неизвестен.

Составляющие ускорения полюса 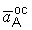и 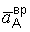были определены выше.

Модуль осестремительной составляющей 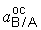легко найти, так как w _АВ определена ранее (см. п. 2 решения):

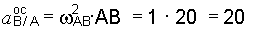см/с².

Модуль вращательной составляющей 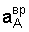неизвестен, так как в выражении

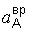= e _АВ х АВ

угловое ускорение e _АВ не может быть найдено до решения векторного уравнения (л). Дифференцирование выражения 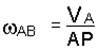здесь не дает результата, так как расстояние АР – величина переменная и закон ее изменения нам неизвестен.

Итак, в векторном уравнении (л) осталось две неизвестные величины – e _ВО1, в выражении 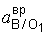(в левой части уравнения) и e _АВ в выражении 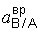(в правой части уравнения). Задача относится к типу 3 (см. п. 3.2.2).

Проектируем уравнение (л) на оси х и у (см. рис. 3.40):

,

.

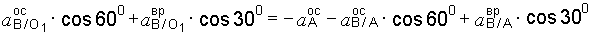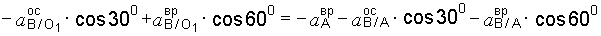Решая полученную систему уравнений, найдем

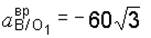см/с²,

.

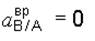Знак “минус” в выражении вращательного ускорения 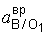указывает, что вектор 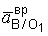направлен в сторону, противоположную принятому на рис. 3.40 направлению.

Полное ускорение точки В:

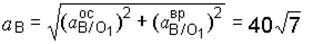см/с²;

угловое ускорение звена АВ

.

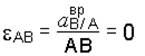У звена АВ теперь нам известны ускорение полюса А, угловая скорость и угловое ускорение звена. Это позволяет определить ускорение любой точки звена, например, точки С (задача типа 1).

Составим для точки С векторное уравнение типа (3.10):

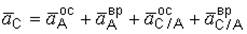. (м)

Ускорение точки С неизвестно по направлению, разложим его на составляющие по направлениям координатных осей а _Сх и a _Cy. Направления остальных векторов из уравнения (м) показаны на рис. 3.40, где

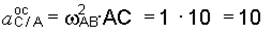см/с²,

.

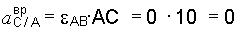Проектируя векторное уравнение (м) на оси координат, получим

;

.

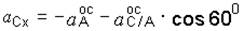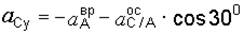Отсюда

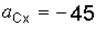см/с².

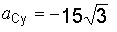см/с².

Полное ускорение точки С:

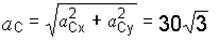см/с².

5. Решение задачи определения ускорений звена ВО₁, совершающего вращательное движение.

По модулю вращательной составляющей 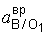, найденному из решения векторного уравнения (л), определим угловое ускорение стержня ВО₁

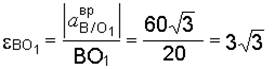1/с².

Направлено угловое ускорение звена ВО₁, в соответствии с действительным направлением вектора 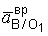(см. замечание по поводу знака 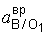), т.е. дуговую стрелку e _ВО1 надо направить по часовой стрелке.

В рассмотренном примере основное векторное уравнение типа (3.10) для точки В преобразовано из обычного вида в уравнение (л), в котором неизвестными являются два угловых ускорения e _АВ и e _ВО1. Подчеркнем, что уравнение (л) получилось в результате приравнивания двух различных выражений для ускорения точки В: первое выражение (и) записано в предположении, что точка В принадлежит звену АВ; второе (к), – что точка В принадлежит звену ВО₁.

С уравнениями вида (л) приходится встречаться в тех случаях, когда точка В в плоском стержневом механизме является центром шарнира, соединяющего два звена, из которых одно совершает плоскопараллельное движение, а второе – вращательное движение.

Date: 2015-09-18; view: 971; Нарушение авторских прав