Задача 3.10 (17)

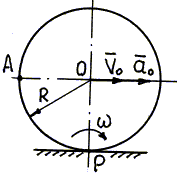Рис. 3.20

Колесо радиуса R = 0,5 м катится без проскальзывания по прямолинейному рельсу (рис. 3.20), имея в данный момент времени скорость центра V0 = 1 м/с и ускорение центра а 0 = 2 м/с2. Определить ускорение точки А обода колеса.

Решение

1. В качестве полюса выберем точку О – центр колеса, ускорение которого известно.

2. Составим основное векторное уравнение типа (3.10) для определения ускорения точки А:

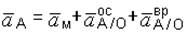. (б)

3. Изобразим все векторы, входящие в уравнение (б), на рис. 3.21.

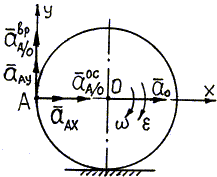Рис. 3.21.

Ускорение точки А, неизвестное по направлению, представим составляющими по направлению координатных осей –` а Ах и` а Ау. Направление ускорения полюса О задано условием задачи. Осестремительное ускорение точки А при вращении вокруг полюса О 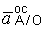направим от точки А к полюсу. Вращательное ускорение точки А при вращении вокруг полюса направим перпендикулярно осестремительному в сторону дуговой стрелки углового ускорения, то есть вертикально вверх (колесо катится ускоренно, поэтому направления дуговых стрелок w и e совпадают).

4. Приступим к анализу векторного уравнения (б). Неизвестными векторного уравнения являются составляющие ускорения точки А:` а <sub>Ах</sub> и` а _Ау, которые не могут быть найдены по условию задачи до решения уравнения (б). Следовательно, все остальные составляющие уравнения (б) должны быть найдены до решения этого уравнения. Ускорение полюса О известно. Остается найти угловую скорость колеса w и угловое ускорение e, чтобы потом определить модули осестремительного и вращательного ускорений точки А при вращении вокруг полюса [см. формулы (3.11) и (3.12)].

При определении скоростей было указано (см. задачу 3.3), что мгновенный центр скоростей колеса известен, это точка касания колеса с рельсом. Зная скорость центра колеса, несложно определить угловую скорость колеса в любой момент времени (рис. 3.20):

. (в)

В данном случае 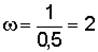1/с.

При качении колеса без проскальзывания расстояние OP от центра колеса до мгновенного центра скоростей остается неизменным (оно равно радиусу колеса). Это обстоятельство дает возможность определить угловое ускорение колеса путем дифференцирования уравнения (в):

,

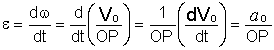т.е. .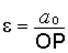

В данном случае 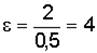1/с².

Зная w и e, определим модули осестремительного и вращательного ускорений точки А при вращении вокруг полюса О:

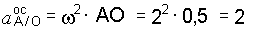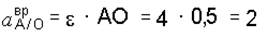м/с²;

м/с².

5. Проектируя теперь векторное уравнение (б) на оси координат, получим:

;

.

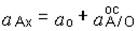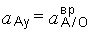1. Подставляя численные значения, найдем:

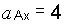м/с²;

м/с².

Полное ускорение точки А: 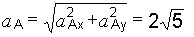м/с².

Date: 2015-09-18; view: 504; Нарушение авторских прав