Уравнения Лагранжа II-го рода

Чтобы найти уравнения движения механической системы в обобщённых координатах, обратимся к общему уравнению динамики, которое даёт

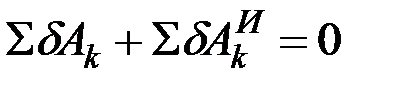. (12.15)

Для общности не будем предполагать, что все наложенные на систему связи являются идеальными. Поэтому в первую сумму могут входить как работы активных сил, так и, например, работы сил трения.

Пусть система имеет s степеней свободы, и её положение определяется обобщёнными координатами. Тогда по формуле (12.7)

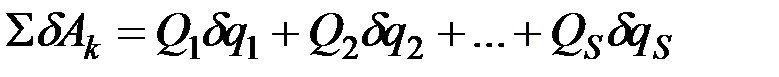. (12.16)

Преобразовав элементарную работу сил инерции , получим

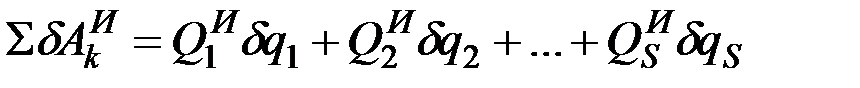, (12.17)

где – это обобщенные силы инерции, которые, согласно формулам (12.10), (12.6), будут равны

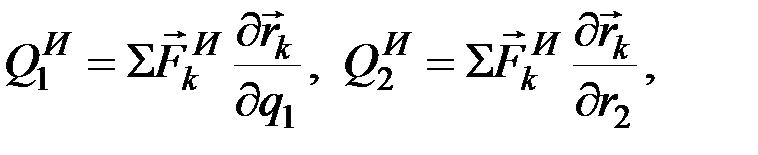… (12.18)

Подставив величины (12.17) и (12.18) в уравнение (12.15), найдём

.

Так как все 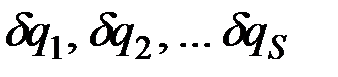между собой независимы, то полученное равенство может выполняться тогда и только тогда, когда каждый из коэффициентов при в отдельности равен нулю, в чем убеждаемся, рассуждая так же, как при выводе уравнений (12.12). Следовательно, должно получиться

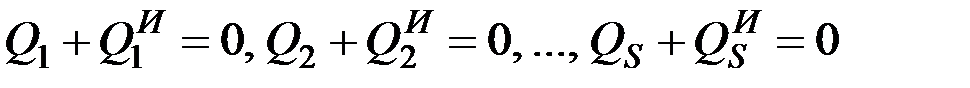(12.19)

Полученными уравнениями можно пользоваться непосредственно для решения задач динамики. Однако процесс составления этих уравнений значительно упростится, если выразить все входящие сюда обобщённые силы инерции через кинетическую энергию системы. Преобразуем сначала соответствующим образом величину 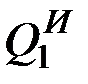. Поскольку сила инерции любой из точек системы равна

,

то в соответствии с первой из формул (12.18) получим

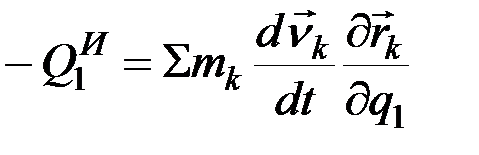. (12.20)

Чтобы выразить 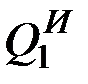через кинетическую энергию системы, необходимо преобразовать правую часть равенства (12.20) так, чтобы она содержала только скорости точек системы. С этой целью заметим прежде всего, что

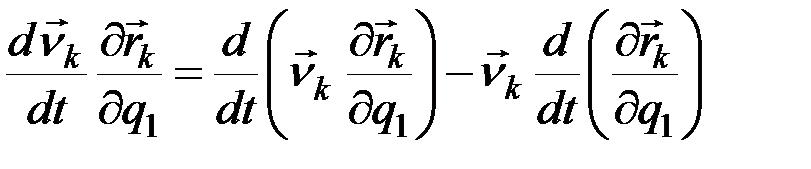. (12.21)

В справедливости равенства (12.21) легко убедиться, продифференцировав произведение, стоящее справа в скобках. Дальнейшее преобразование осуществляется с помощью следующих двух равенств:

и 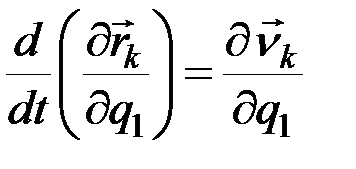. (12.22)

Докажем сначала справедливость первого из них. Так как, согласно (12.1), 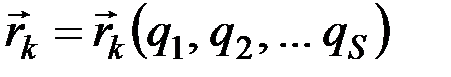, то

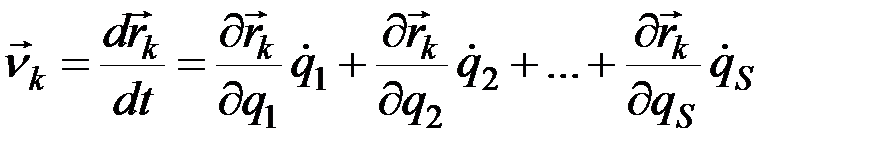
и

.

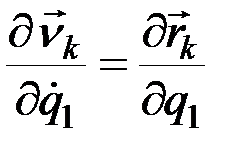Справедливость второго из равенств (12.22) доказывается тем, что операции полного дифференцирования по t и частного по 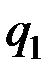переместительны, т.е.

.

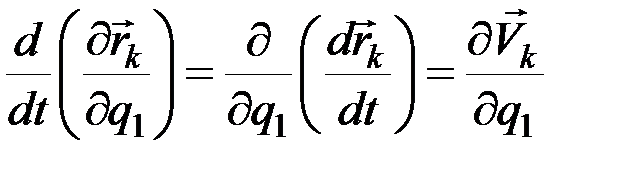Подставив величины из выражения (12.22) в равенство (12.21), получим

,

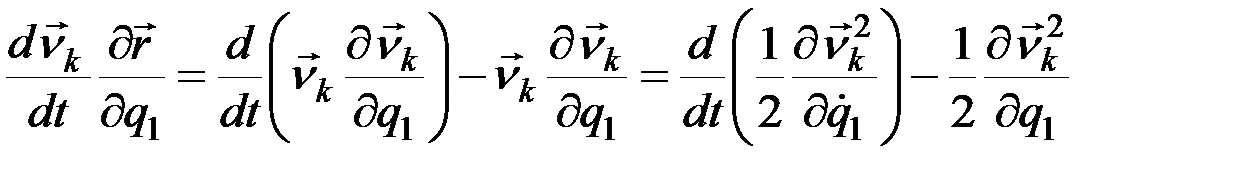и формула (12.20), если учесть, что сумма производных равна производной от суммы примет вид:

,

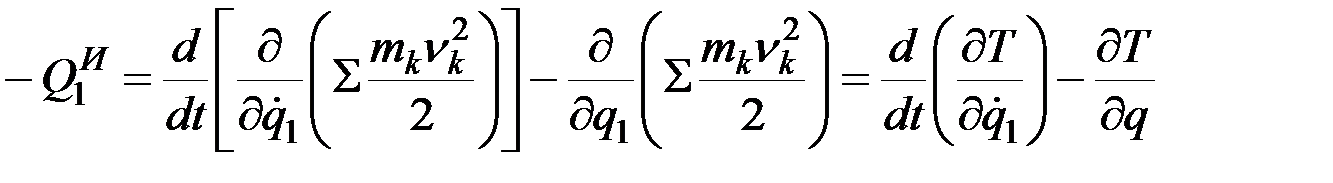где 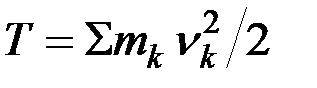– кинетическая энергия системы.

Аналогичные выражения получаются для всех остальных обобщенных сил инерции. В результате равенства (12.19) дадут окончательно

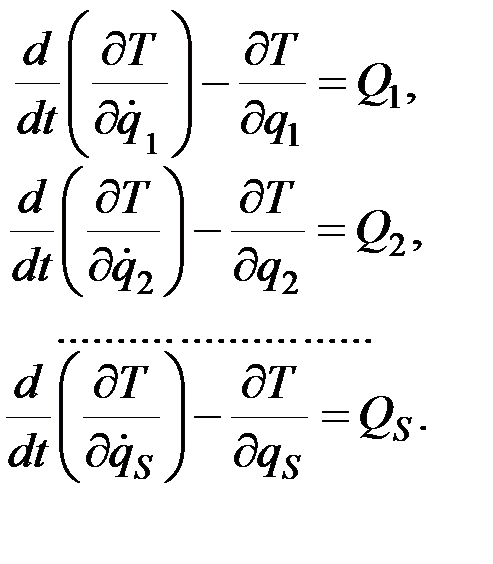(12.23)

Уравнения (12.23) представляют собой дифференциальные уравнения движения системы в обобщённых координатах или уравнения Лагранжа II-го рода (в частных производных). Число этих уравнений, как видим, равно числу степеней свободы системы.

Уравнения Лагранжа дают единый и притом достаточно простой метод решения задач динамики. Важное преимущество этих уравнений состоит в том, что их вид и число не зависят ни от количества тел (или точек), входящих в рассматриваемую систему, ни от того, как эти тела движутся; число уравнений Лагранжа равно числу степеней свободы системы. Кроме того, при идеальных связях в правые части уравнений (12.23) входят обобщённые активные силы, и, следовательно, эти уравнения позволяют исключить из рассмотрения все заранее неизвестные реакции связей.

Основная задача динамики в обобщённых координатах состоит в том, чтобы, зная обобщённые силы 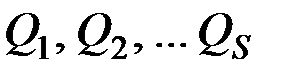и начальные условия, найти закон движения системы в виде (12.2), т.е. определить обобщённые координаты 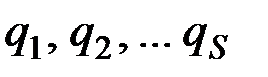как функции времени.

Случай потенциальных сил. Если действующие на систему силы потенциальны, то, используя формулы (12.10), можно первые из уравнений (12.23) представить в виде

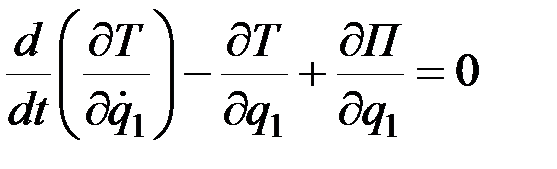
или

.

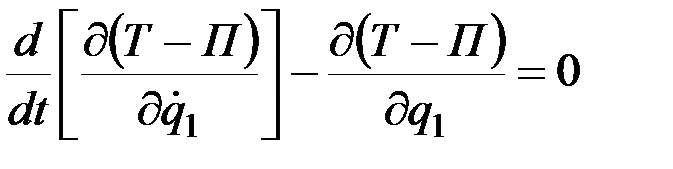Последнее равенство справедливо потому, что потенциальная энергия П зависит только от координат , а от обобщенных скоростей не зависит, следовательно, .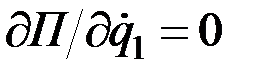

Аналогично преобразуются все остальные уравнения системы (12.23). Введём функцию

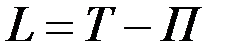. (12.24)

Функция 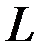от обобщённых координат и обобщённых скоростей, равная разности между кинематической и потенциальной энергиями системы, называется функцией Лагранжа или кинематическим потенциалом. Тогда в случае потенциальных сил уравнения Лагранжа примут вид:

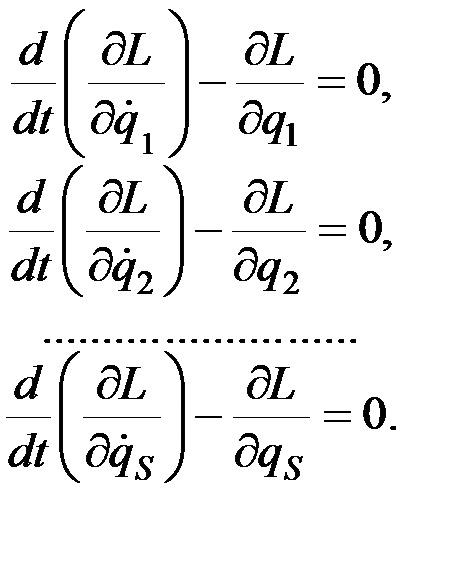(12.25)

Из полученного результата следует, что состояние механической системы, на которую действуют потенциальные силы, определяются заданием одной только функции Лагранжа, так как, зная эту функцию, можно составить дифференциальные уравнения движения системы.

При соответствующем обобщении понятий функции аналогичные функции Лагранжа описывают состояние других физических систем (непрерывной среды, гравитационного или электромагнитного поля и др.). Поэтому уравнения Лагранжа вида (12.25) играют важную роль в ряде областей физики.

Уравнениями Лагранжа можно пользоваться при изучении движения любой механической системы с геометрическими или сводящимися к геометрическим (голономными) связями, независимо от того, сколько тел (или точек) входит в систему, как движутся эти тела, и какое движение (абсолютное или относительное) рассматривается.

Чтобы для заданной механической системы составить уравнения Лагранжа, необходимо:

1) установить число степеней свободы системы и выбрать обобщённые координаты;

2) изобразить систему в произвольном положении и показать на рисунке все действующие силы (для системы с идеальными связями – только активные);

3) вычислить обобщённые силы 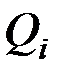, при этом, во избежание ошибок в знаках, каждое сообщаемое системе возможное перемещение должно быть направлено так, чтобы приращение соответствующей координаты было положительным;

4) определить кинетическую энергию 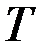системы в её абсолютном движении и выразить эту энергию через обобщённые координаты 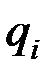и обобщённые скорости ;

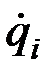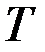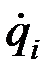5) определить соответствующие частные производные от по и 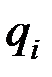, затем подставить все значения в уравнения (12.23).

Указанным путем уравнения Лагранжа составляются независимо от того, рассматривается ли абсолютное (по отношению к инерциальной системе отсчёта) или относительное движение механической системы.

При рассмотрении относительного движения механической системы возможен и другой путь: кинетическую энергию системы определять в её относительном движении, но зато при определении обобщённых сил присоединить к силам, действующим на систему, переносные силы инерции, чего при использовании первого пути делать не следует.

Из полученных уравнений, если заданы действующие силы и начальные условия, можно, интегрируя эти уравнения, найти закон движения системы в виде (12.2). Если же задан закон движения, то составленные уравнения позволяют определить действующие силы.

В случае, когда все приложенные к системе силы являются потенциальными, уравнения Лагранжа можно составлять в виде уравнения (12.25). При этом вместо вычисления обобщённых сил следует определить потенциальную энергию системы, выразив её через обобщённые координаты, и затем, определив ещё и кинетическую энергию, составить функцию Лагранжа (12.24).

Пример 10. Составить, воспользовавшись методом Лагранжа, дифференциальное уравнение колебаний физического маятника (п. 8.8).

Решение. Маятник имеет одну степень свободы, и его положение определяется углом 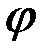(рис. 33). Следовательно, 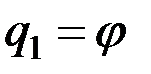. Сообщив углу 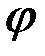положительное приращение 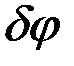, найдём, что на этом перемещении работу совершает только сила тяжест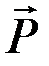и и

,

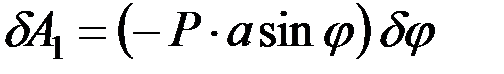где .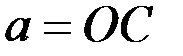

Поэтому

.

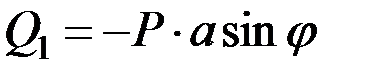Кинетическая энергия маятника равна

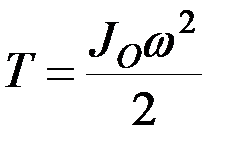
или

.

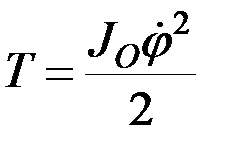Напомним, что величина 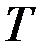должна быть выражена через обобщённую скорость, а . Так как 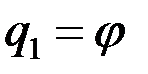, уравнение Лагранжа имеет вид

.

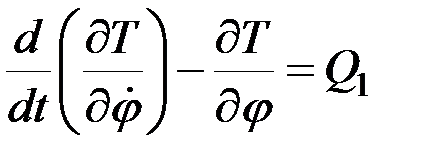В данном случае, поскольку 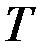от угла 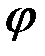не зависит, то

,

,

.

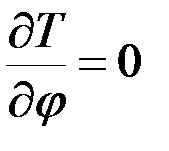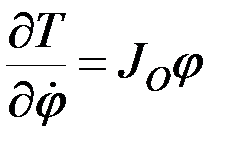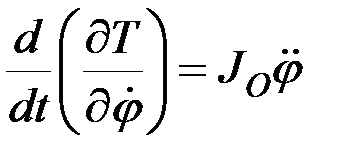Подставив найденные величины в уравнение Лагранжа, получим

,

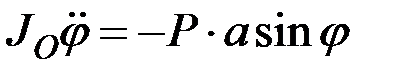т.е. тот же результат, что и в пункте 8.8.

Поскольку сила тяжести 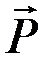потенциальна, то уравнение Лагранжа можно составить в виде (12.25). Направляя ось 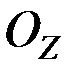вертикально вниз, имеем в данном случае

.

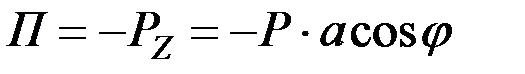Тогда по формуле (12.24)

,

,

.

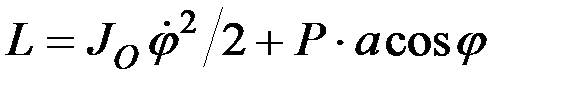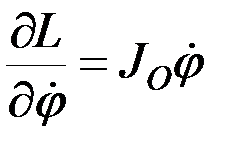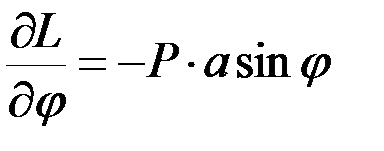В соответствии с уравнениями (12.25) получим

.

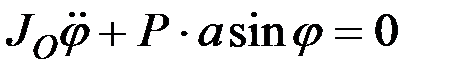Пример 11. Масса тележки 1равна , масса находящегося на ней сплошного цилиндрического катка 2 равна . Определить, с каким ускорением будет двигаться тележка вдоль горизонтальной плоскости под действием приложенной к ней силы (рис. 41), если каток при этом катится по тележке без скольжения. Массой колес тележки пренебречь.

Рис. 41

Решение. Система имеет две степени свободы (независимы друг от друга перемещение катка относительно тележки и перемещение самой тележки). В качестве обобщённых координат выберем координату 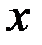тележки и координату 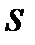центра масс С катка относительно тележки. Тогда уравнения Лагранжа для системы будут иметь вид:

,

.

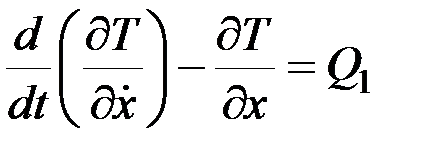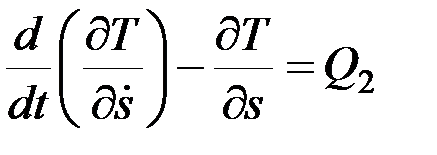Кинетическая энергия тележки равна

,

а катка

,

где 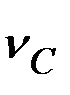– абсолютная скорость центра С катка, равная

.

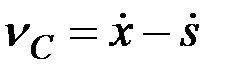Так как для сплошного цилиндра 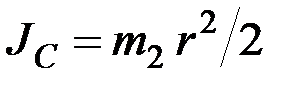, а при качении без скольжения 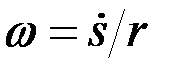, где 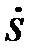– относительная скорость центра 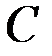по отношению к тележке (считать здесь было бы ошибкой), то окончательно получим

.

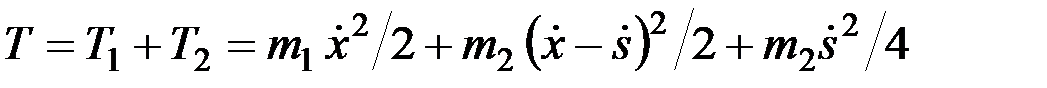Тогда

,

,

.

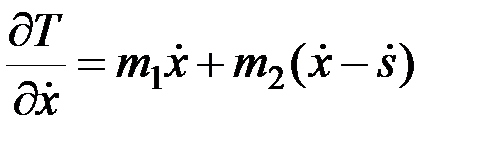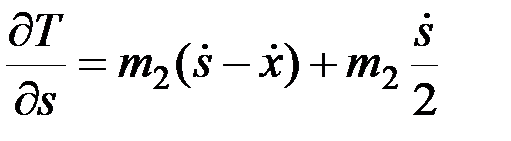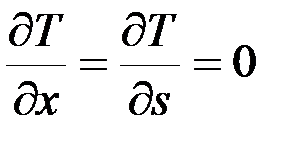Для определения обобщённых сил сначала сообщим системе возможное перемещение, при котором координата 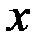получит приращение 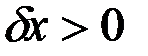. На этом перемещении 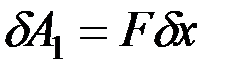. На перемещении же, при котором 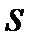получит приращение 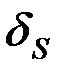, очевидно, . Следовательно,

, .

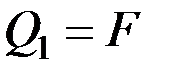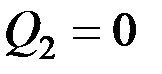Подставив эти значения в выражения для производных, найдём следующие дифференциальные уравнения движения системы:

,

.

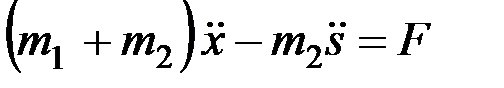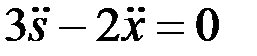Из последнего уравнения

,

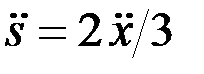и тогда окончательно получим для ускорения тележки выражение

.

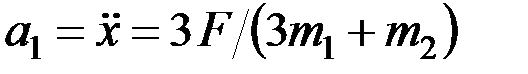Если каток был бы на тележке закреплён неподвижно, то её ускорение, очевидно, равнялось бы

.

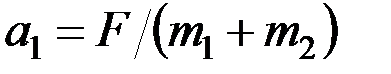Отметим еще один результат. Допустим, что трения катка о тележку нет. Тогда он по тележке будет скользить, двигаясь поступательно, и

.

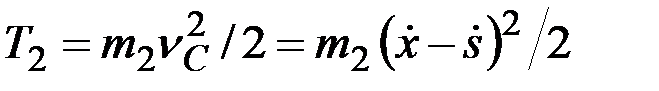В результате для системы

.

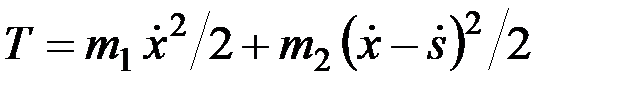Легко определить, что первое из уравнений при этом не изменится, а второе при

,

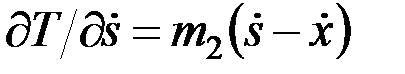примет вид

,

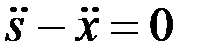откуда

.

В результате из первого уравнения системы находим для ускорения тележки выражение

.

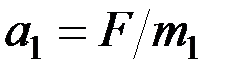Объясняется такой результат тем, что при отсутствии трения тележка движется так же, как если бы катка на ней вообще не было.

Контрольные вопросы и задания

1. Что такое обобщённая координата?

2. Что такое обобщённая скорость?

3. Что называется обобщённой силой?

4. Какова размерность обобщённой силы?

5. Как определить обобщённую силу?

6. Какие силы называются потенциальными?

7. Как определить обобщённую силу в случае потенциальных сил?

8. Как формулируются условия равновесия механической системы в обобщённых координатах?

9. Запишите уравнение Лагранжа второго рода для системы с одной степенью свободы.

10. В чем состоит физический смысл уравнения Лагранжа второго рода?

11. Как определить количество уравнений Лагранжа, необходимых для описания движения механической системы?

12. В какой форме записываются уравнения Лагранжа второго рода в случае потенциальных сил?

13. Какое значение имеют уравнения Лагранжа при решении практических задач?

14. Какова последовательность решения задач при использовании уравнений Лагранжа второго рода?

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Тарг, С. М. Краткий курс теоретической механики: учеб. для втузов / С. М. Тарг – 12-е изд., стереотип. – М.: Высшая школа, 1998. – 415 с.

2. Бутенин, Н. В. Курс теоретической механики: учеб. для втузов: в 2-х т. / Н. В. Бутенин, Я. Л. Лунц, Д. Р. Меркин. – 3-е изд., испр. – М., 1985 (и последующие издания).

3. Яблонский, А. А. Сборник заданий для курсовых работ по теоретической механике: учеб. пос. для втузов / А. А. Яблонский, С. С. Норейко, С. А. Вольфсон и др. / под ред. А. А. Яблонского. – 4-е изд., перераб. и доп. – М.: Высш. шк., 1985. – 367 с. (и последующие издания).

4. Мещерский, И. В. Сборник задач по теоретической механике: учеб. пос. для втузов / И. В. Мещерский / под ред. Н. В. Бутенина, А. И. Лурье, Д. Р. Меркина. – 36-е изд., испр. – М.: Наука, 1986. – 448 с.

5. Бать, М. И. Теоретическая механика в примерах и задачах: учеб. пос. для втузовв в 3-х т. / М. И. Бать, Г. Ю. Джанелидзе, А. С. Кельзон. – 9-е изд., перераб. – М.: Наука, Гл.. ред. физ.-мат. лит., 1990.

6. Вильке, В. Г. Теоретическая механика: учебник / В. Г. Вильке. – 2-е изд., перераб. и доп. – М.: Изд-во МГУ, 2000. – 719 с.

7. Голубев, Ю. Ф. Основы теоретической механики: учеб. для студ. высш. учеб. заведений / Ю. Ф Голубев.– 2-е изд., перераб. и доп. – М.: МГУ, 2000. – 719 с.

8. Цивильский, В. Л. Теоретическая механика: учеб. для вузов / В. Л. Цивильский. – М.: Высшая школа, 2001. – 319 с.

9. Яблонский, А. А. Курс теоретической механики: учеб. для тех. вузов / А. А. Яблонский, В. М. Никифорова. – 7-е. изд. – СПб: Лань, 1999. – 768 с.

10. Аркуша, А. И. Руководство к решению задач по теоретической механике: учеб. пос. для студ. сред. спец. учеб. заведений / А. И. Аркуша. – 7-е изд., стереотип – М.: Высшая школа, 2004. – 336 с.: ил.

11. Мещерский, И. В. Задачи по теоретической механике: учеб. пос. для студ. высш. учеб. заведений / И. В. Мещерский. – 39-е изд., стереотип. – М.: Лань, 2002. – 448 с.

12. Уиттекер, Э. Т. Аналитическая динамика / пер. с англ.– Ижевск: Изд. дом «Удмуртский университет», 1999. – 588 с.

13. Арнольд, В. И. Математические методы классической механики: учеб. пос. для студ. / В. И. Арнольд. – 5-е. изд., стереотип. – М.: УРСС, 2003. – 416 с.

14. Серегин, Г. В. Техническая механика. Теоретическая механика: программа, методические указания и контрольные работы / Г. В. Серегин, В. М. Потапов, Е.Н. Миронов. – Новосибирск: Изд. НГПУ, 1997. – 47 с.

15. Потапов, В. М. Основы техники: учеб. пос. / В. М. Потапов, В. В. Крашенинников. – Новосибирск: Изд. НГПУ, 1999. – 52 с.

16. Потапов, В. М. Введение в прикладную механику: учеб. пос. / В. М. Потапов, В. В. Крашенинников, И. Н. Лукина, Е. Н. Миронов. – Новосибирск.: Изд. НГПУ, 2003. – 180 с.

17. Бутенин, Н. В. Введение в аналитическую механику: учеб. пос. / Н. В. Бутенин, Н. А. Фуфаев. – 2-е изд., перераб. и доп. – М.: Наука, Гл. ред. физ.-мат. лит., 1991. – 256 с.

18. Добронравов, В. В. Основы аналитической механики: учеб. пос. для вузов / В. В. Добронравов. – М.: Высшая школа, 1976. – 263 с.: ил.

19. Ландау, Л. Д. Теоретическая физика: учеб. пос. для физ. специальностей ун-тов / Л. Д. Ландау, Е. М. Лифшиц. – Изд. 3-е., испр. и доп. – М.: Наука, 1973. – 208 с.: ил. – Т.1. Механика.

20. Никитин, Н. Н. Курс теоретической механики: учеб. для машиностроит. и приборостроит. спец. вузов / Н. Н. Никитин. – 5-е изд., перераб. и доп. – М.: Высшая школа, 1990. – 606 с.:ил.

21. Савельев, И. В. Основы теоретической физики / И. В. Савельев.– М.: Наука, 1991. – 493 с.: ил. – Т.1. Механика. Электродинамика.

22. Бражниченко, Н. А. Сборник задач по теоретической механике: учеб. пос. для вузов / Н. А. Бражниченко, В. Л. Кан, Б. Л. Минцберг, В. И. Морозов / под ред. Н. А. Бражниченко. – 4-е изд., испр. – М.: Высшая школа, 1986. – 480 с.: ил.

23. Кепе, О. Э. Сборник коротких задач по теоретической механике: учеб. пос. / О. Э. Кепе, Я. А. Виба, О. П. Грапис и др. / под ред. О. Э. Кепе. – М.: Высшая школа, 1989.– 368 с.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ....................................................................................................... 3

1. ЗАКОНЫ ГАЛИЛЕЯ–НЬЮТОНА........................................................... 5

2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ В ДЕКАРТОВЫХ КООРДИНАТАХ... 11

2.1. Прямолинейное движение точки..................................................... 12

2.2. Криволинейное движение точки..................................................... 13

3. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ........ 15

3.1. Виды колебательных движений материальной точки................. 15

3.2. Свободные колебания точки без учёта сил сопротивления....... 16

3.3. Свободные колебания при сопротивлении,
пропорциональном скорости (затухающие колебания)..................... 19

3.4. Вынужденные колебания. Резонанс................................................ 24

4. ДВИЖЕНИЕ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ. СВЯЗИ И ДИНАМИЧЕСКИЕ РЕАКЦИИ СВЯЗЕЙ.............................................. 30

5. СИСТЕМА МАТЕРИАЛЬНЫХ ТОЧЕК. ТВЁРДОЕ ТЕЛО.............. 36

6. МОМЕНТЫ ИНЕРЦИИ ТВЁРДОГО ТЕЛА......................................... 40

6.1. Моменты инерции твёрдого тела относительно
осей координат........................................................................................... 40

6.2. Моменты инерции тела относительно параллельных осей. Теорема Гюйгенса – Штейнера............................................................................... 46

6.3. Центробежные моменты инерции. Главные оси инерции тела.. 48

7. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС....................................... 51

8. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ....................................................................................................................... 54

8.1. Теорема об изменении количества движения точки.................... 55

8.2. Две меры механического движения. Работа силы. Мощность... 56

8.3. Теорема об изменении кинетической энергии точки................... 60

8.4. Моменты количества движения материальной точки относительно центра и относительно оси....................................................................................... 63

8.5. Теорема об изменении момента количества движения материальной точки....................................................................................................................... 65

8.6. Кинетическая энергия твёрдого тела.............................................. 70

8.7. Теорема об изменении кинетической энергии системы............... 74

8.8. Физический маятник.......................................................................... 77

9. ПРИНЦИП ДАЛАМБЕРА........................................................................ 82

9.1. Принцип Даламбера для точки и механической системы........... 82

9.2. Главный вектор и главный момент сил инерции.......................... 85

9.3. Приведение сил инерции твёрдого тела......................................... 86

10. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ................................. 92

10.1. Возможные перемещения системы. Число степеней свободы. 92

10.2. Принцип возможных перемещений для механической системы 94

11. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ................................................ 100

12. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЁННЫХ КООРДИНАТАХ. УРАВНЕНИЯ ЛАГРАНЖА II-го РОДА 104

12.1. Обобщённые координаты и обобщенные скорости................. 104

12.2. Обобщённые силы......................................................................... 105

12.3. Условия равновесия системы в обобщённых координатах.... 110

12.4. Уравнения Лагранжа II-го рода................................................... 111

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА...................................................... 123

Учебное издание

Владимир Васильевич Алексеев

Александр Всеволодович Кириллов

Владимир Михайлович Потапов

Наталья Дмитриевна Бондаренко

Date: 2015-09-03; view: 1739; Нарушение авторских прав