Приведение сил инерции твёрдого тела

Систему сил инерции твёрдого теламожно заменить одной силой, равной 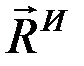и приложенной в произвольно выбранном центре О, и парой с моментом, равным . Рассмотрим несколько частных случаев.

Поступательное движение. В этом случае ускорения всех точек тела одинаковы и равны ускорению центра масс 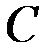тела 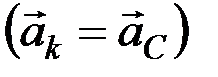. Тогда все силы инерции образуют систему параллельных сил, аналогичных силам тяжести , и поэтому, как и силы тяжести, имеют равнодействующую, проходящую через точку .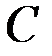

Следовательно, при поступательном движении силы инерции твёрдого тела приводятся к равнодействующей, равной , проходящей через центр масс тела.

Вращательное движение. Пусть твёрдое тело имеет плоскость материальной симметрии Оxy и вращается вокруг оси О_z, перпендикулярной этой плоскости (на рис. 34 показано сечение тела плоскостью Оxy). Если привести силы инерции к центру О, то вследствие симметрии результирующая сила и пара будут лежать в плоскости Оxy,и момент пары будет равен 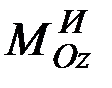. Следовательно, так как кинетический момент вращающегося тела равен , то в соответствии со второй из формул (9.9) имеем:

, (9.10)

где 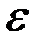– угловое ускорение тела.

Рис. 34

Следовательно, система сил инерции вращающего тела приводится к силе 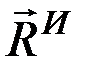, определяемой формулой (9.7) и приложенной в точке О (рис. 34), и к паре с моментом 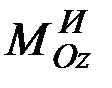, определяемым формулой (9.10), лежащей в плоскости симметрии тела.

Вращение вокруг оси, проходящей через центр масс тела. Если тело вращается вокруг оси С_z, проходящей через центр масс С тела, то 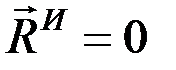, так как 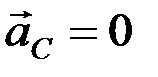. Следовательно, в этом случае система сил инерции тела приводится к одной только паре с моментом 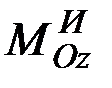, лежащей в плоскости симметрии тела.

Плоскопараллельное движение. Если тело имеет плоскость симметрии и движется параллельно этой плоскости, то, очевидно, система сил инерции тела приведется к лежащим в плоскости симметрии силе, равной и приложенной в центре масс С тела, и паре с моментом .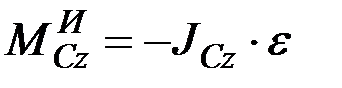

При решении задач по формулам вида (9.10) вычисляются модуль момента 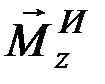, а его направление, противоположное , указывается на чертеже.

Пример 5. Два груза весом и 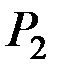каждый, связанные нитью, движутся по горизонтальной плоскости под действием силы , приложенной к первому грузу (рис. 35, а). Коэффициент трения грузов о плоскость f. Определить ускорение грузов и натяжение нити.

Рис. 35

Решение. Изобразим все действующие на систему внешние силы. Прибавим к этим силам силы инерции грузов. Так как оба груза движутся поступательно с одним и тем же ускорением, то по модулю

, .

Направления сил показаны на чертеже. Силы трения равны:

, .

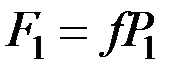Согласно принципу Даламбера, полученная система сил должна находиться в равновесии. Составляя уравнение равновесия в проекции на горизонтальную ось, найдём

.

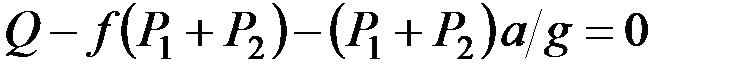Отсюда

.

Очевидно, грузы будут двигаться, если .

Искомое натяжение нити является в рассматриваемой системе силой внутренней. Для её определения расчленим систему и применим принцип Даламбера к одному из грузов, например, ко второму (рис. 35, б). На этот груз действует сила , нормальная реакция , сила трения 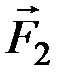и натяжение нити 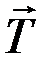. Присоедив к ним силу инерции 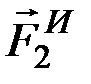и составив уравнения равновесия в проекции на горизонтальную ось, найдём

.

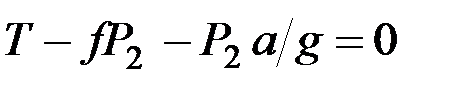Подставив найденное ранее значение 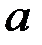, получим окончательно

.

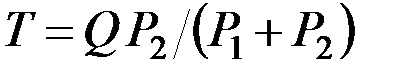Интересно, что натяжение нити в этом случае не зависит от силы трения и при одном и том же суммарном весе системы будет тем меньше, чем меньше вес второго (заднего) груза. Поэтому, например, в железнодорожном составе выгоднее в голове помещать более тяжелые вагоны, а в хвосте – более легкие.

Рассмотрим численный пример. Пусть , , 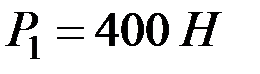. Тогда движение возможно, если . Натяжение нити при этом равно 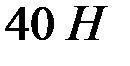. Если грузы поменять местами, то натяжение нити станет равным .

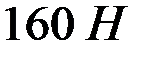Пример 6. Однородный стержень АВ весом 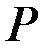, закреплённый в точке А шарниром, отклоняют до горизонтального положения и отпускают без начальной скорости (рис. 36). Определить реакцию шарнира А как функцию угла .

Рис. 36

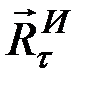Решение. Рассмотрев стержень в произвольном положении, проведём оси Аxy (перпендикулярно стержню и вдоль стержня) и изобразим действующие на стержень силу тяжести и реакции , . Используя принцип Даламбера, присоединим к этим силам силы инерции стержня, приведя их к центру А. Тогда силы инерции будут представлены двумя составляющими и 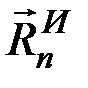главного вектора 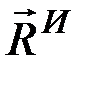и парой с моментом 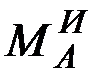. При этом по формулам (9.8) и (9.10) модули этих составляющих и момента пары имеют значения:

,

,

,

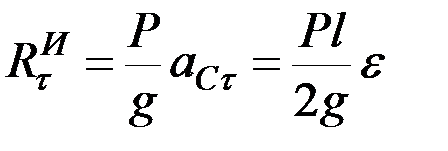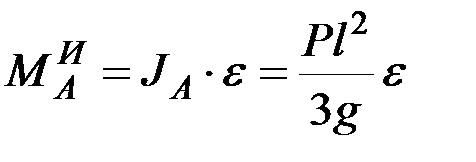где l – длина стержня, и 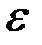– его угловая скорость и угловое ускорение.

Составив для этой плоской системы сил уравнения равновесия 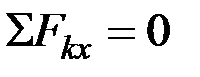, , 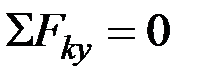, 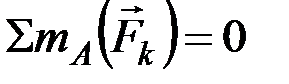получим:

,

,

.

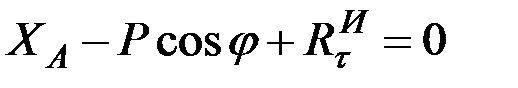Из последнего уравнения, заменив его значением, найдём :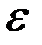

.

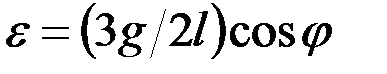Для определения величины , входящей в выражение , можно или проинтегрировать это уравнение, или воспользоваться теоремой об изменении кинетической энергии. Выбирая второй путь и учитывая, что Т ₀ = 0, получаем:

или

,

откуда

.

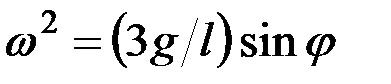При найденных значениях и

,

.

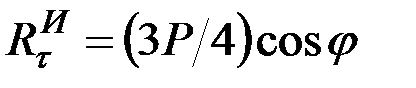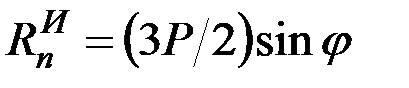Подставив эти величины в уравнения, найдём искомые реакции:

,

.

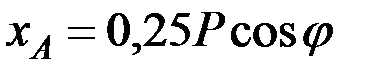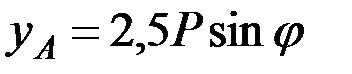В начальный момент времени 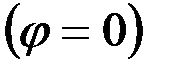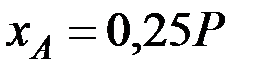, . В момент времени, когда стержень проходит через вертикаль , .

Контрольные вопросы

1. Как определить силу инерции?

2. В чем состоит принцип Даламбера для материальной точки?

3. Сформулируйте принцип Даламбера для механической системы.

4. В чем состоит значение принципа Даламбера при решении задач динамики?

5. Как определить главный вектор сил инерции?

6. Как определить главный момент сил инерции?

7. К чему приводят силы инерции в случае простейших движений твёрдого тела (поступательного, вращательного, плоскопараллельного)?

Date: 2015-09-03; view: 946; Нарушение авторских прав