Условия равновесия системы в обобщённых координатах

Согласно принципу возможных перемещений необходимым и достаточным условием равновесия механической системы является равенство нулю суммы элементарных работ всех активных сил (и сил трения, если они совершают работу) на любом возможном перемещении системы, т.е. . В обобщённых координатах это условие, согласно равенству (12.7), даёт

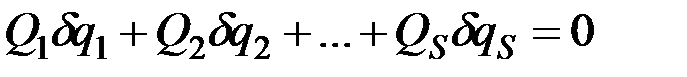. (12.11)

Так как все величины 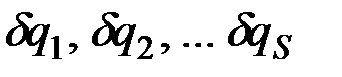друг от друга независимы, то равенство (12.11) может выполняться тогда и только тогда, когда каждый из коэффициентов при 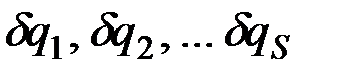в отдельности равен нулю, т.е.

. (12.12)

В самом деле, если допустить, что одна из этих величин, например 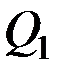, не равна нулю, то всегда можно сообщить системе такое возможное перемещение, при котором 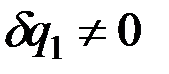, а 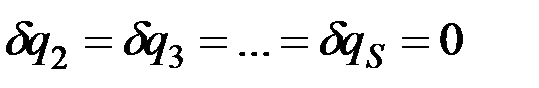, что противоречит условию (12.11).

Таким образом, для равновесия механической системы необходимо и достаточно, чтобы все обобщённые силы, соответствующие выбранным для системы обобщённым координатам, были равны нулю. Число условий равновесия (12.12) равно,как видим, числу обобщённых координат, т.е. числу степеней свободы системы.

Случай потенциальных сил. В этом случае условия равновесия (12.12), если учесть равенства (12.9) и (12.10), дают

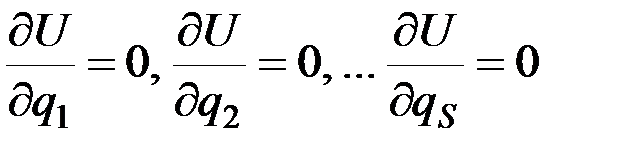(12.13)

или

.

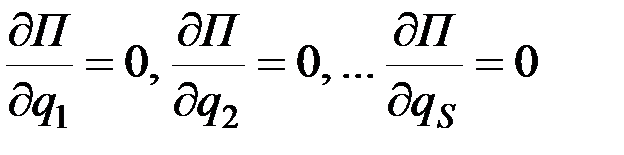Отсюда следует, что при равновесии полный дифференциал функций U или П равен нулю, т.е.

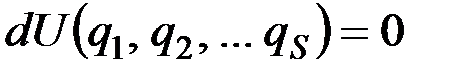
или

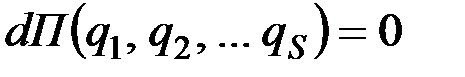. (12.14)

Равенства (12.13) или (12.14) выражают необходимые условия экстремума функции нескольких переменных. Следовательно, система, на которую действуют потенциальные силы, в тех положениях, для которых силовая функция или потенциальная энергия системы имеет экстремум (в частности, минимум или максимум), находится в равновесии.

Date: 2015-09-03; view: 570; Нарушение авторских прав