Возможные перемещения системы. Число степеней свободы

Эффект механических связей можно учитывать, не только вводя в рассмотрение их реакции, как это до сих пор делалось, но и рассматривая те перемещения, которые могут иметь точки механической системы при наложенных на нее связях. Такой путь позволяет сразу получить уравнения равновесия или движения системы, не содержащие заранее неизвестных реакций связей, что существенно облегчает решение многих задач механики.

Перемещения, о которых сказано выше, называют возможными (или виртуальными). Они должны удовлетворять двум условиям:

1) быть элементарными, так как при конечном перемещении система может перейти в положение, где эффект наложенных связей будет другим;

2) быть такими, чтобы все наложенные в данный момент времени на систему связи сохранялись, иначе может измениться вид рассматриваемой механической системы.

Таким образом, возможным перемещением механической системы будем называть любую совокупность элементарных перемещений точек этой системы из занимаемого в данный момент времени положения, которые допускаются всеми наложенными на систему связями. При этом под допускаемыми в случае неудерживающих связей будем понимать те возможные перемещения, при которых связи сохраняются (точки системы от связей не «освобождаются»).

В дальнейшем следует различать действительное перемещение 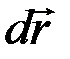движущейся точки, которое она совершает за элементарный промежуток времени 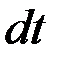, и возможное перемещение, которого точка не совершает, а только могла бы совершить, не нарушая наложенных на неё в данный момент времени связей.

Чтобы учесть это различие, будем обозначать возможное перемещение точки символом 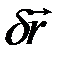и изображать соответствующим элементарным вектором. При этом 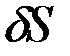будет обозначать модуль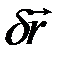 , а , , 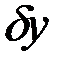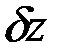– проекции 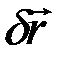на координатные оси; эти проекции равны элементарным приращениям координат точки при её возможном перемещении и формально вычисляются так же, как дифференциалы.

Отметим, что при стационарных связях действительное перемещение 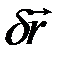любой точки системы совпадает с одним из возможных перемещений. При нестационарных связях 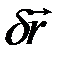ни с одним из возможных перемещений не совпадает.

В общем случае механическая система может иметь множество различных возможных перемещений. Однако для любой из систем, которые нами будут рассматриваться, можно указать некоторое число таких независимых друг от друга перемещений, что всякое другое возможное перемещение может быть через них выражено. Например, для точки, находящейся на какой-нибудь плоскости (поверхности), любое возможное перемещение 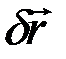вдоль этой плоскости можно выразить через два взаимно перпендикулярных перемещения 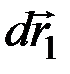и 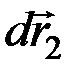в виде

,

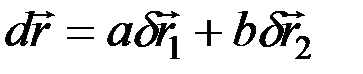где а и b – любые положительные или отрицательные числа.

Число независимых друг от друга возможных перемещений механической системы называется числом степени свободы этой системы.

Следовательно, точка, находящаяся на плоскости, имеет две степени свободы; одновременно её положение на плоскости определяется двумя независимыми координатами (координатами, каждая из которых может изменяться независимо от другой), например, координатами x и y. Свободная материальная точка имеет три степени свободы (независимыми будут три возможных перемещения вдоль трёх взаимно перпендикулярных осей); одновременно положение точки определяется тремя независимыми координатами x, y, z и т.д.

Этот результат оказывается общим, т.е. у механической системы с геометрическими связями число независимых координат, определяющих положение системы, совпадает с числом её степеней свободы. Поэтому у такой системы число степеней свободы можно определять как по числу независимых возможных перемещений, так и по числу независимых координат. Так, у кривошипно-ползунного механизма одна степень свободы (у него одно независимое возможное перемещение, например, поворот кривошипа ОА, и одна независимая координата, например, угол 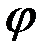). У свободного твёрдого тела шесть степеней свободы (три поступательных вдоль координатных осей и три поворота вокруг этих осей) и шесть независимых координат (три координаты полюса и три угла Эйлера).

Date: 2015-09-03; view: 1003; Нарушение авторских прав