Принцип возможных перемещений для механической системы

Перейдём к рассмотрению еще одного принципа механики, который устанавливает общее условие равновесия механической системы. Под равновесием мы понимаем то состояние системы, при котором все её точки под действием приложенных сил находятся в покое по отношению к инерциальной системе отсчёта (рассматриваем так называемое «абсолютное» равновесие). Одновременно будем считать все наложенные на систему связи стационарными, не оговаривая это каждый раз в дальнейшем.

Введём понятие о возможной работе как об элементарной работе, которую действующая на материальную точку сила могла бы совершить на перемещении, совпадающем с возможным перемещением этой точки. Обозначим возможную работу активной силы 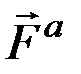символом 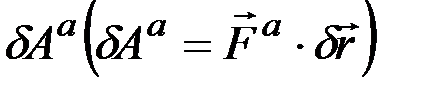, а возможную работу реакции 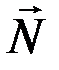связи – символом .

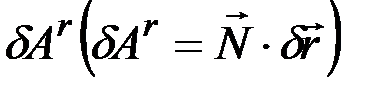Теперь дадим общее определение понятия об идеальных связях, которыми мы уже пользовались: идеальными называются связи, для которых сумма элементарных работ их реакций на любом возможном перемещении системы равна нулю, т.е.

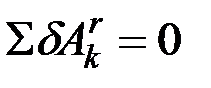. (10.1)

Для определения необходимого условия равновесия докажем, что если механическая система с идеальными связями находится в равновесии под действием положительных сил, то при любом возможном перемещении системы должно выполняться равенство

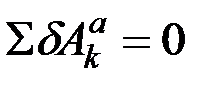(10.2)

или

(10.3)

где – угол между силой и возможным перемещением.

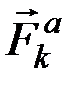Обозначим равнодействующие всех (и внешних, и внутренних) активных сил и реакций связей, действующих на какую-нибудь точку системы , через и 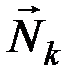. Тогда, поскольку каждая из точек системы находится в равновесии, 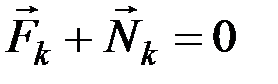, а следовательно, и сумма работ этих сил при любом перемещении точки будет тоже равна нулю, т.е. 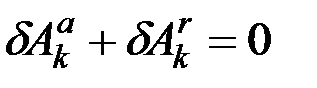. Составив такие равенства для всех точек системы и сложив их почленно, получим

.

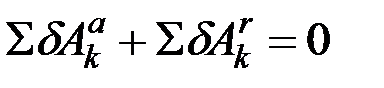Но так как связи идеальные, а представляют собой возможные перемещения точек системы, то вторая сумма по условию (10.1) будет равна нулю. Тогда равна нулю и первая сумма, т.е. выполняется равенство (10.2). Таким образом, доказано, что равенство (10.2) выражает необходимое условие равновесия системы.

Покажем, что это условие является достаточным, т.е. что если к точкам механической системы, находящейся в покое, приложить активные силы , удовлетворяющие равенству (10.2), то система останется в покое. Предположим обратное, что система при этом придёт в движение, и некоторые её точки совершат действительные перемещения . Тогда силы 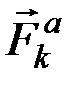совершат на этих перемещениях работу, и, по теореме об изменении кинетической энергии, будем иметь:

,

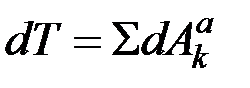
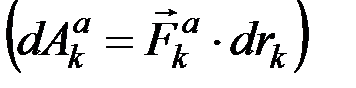где, очевидно, 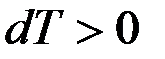, так как вначале система была в покое, следовательно, и . Но при стационарных связях действительные перемещения совпадают с какими-то из возможных перемещений и на этих перемещениях тоже должно быть 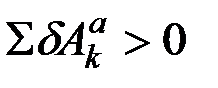, что противоречит условию (10.2). Таким образом, когда приложенные силы удовлетворяют условию (10.2), система из состояния покоя выйти не может, и это условие является достаточным условием равновесия.

Из доказанного вытекает следующий принцип возможных перемещений: для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на неё активных сил при любом возможном перемещении системы была равна нулю. Математически сформированное условие равновесия выражается равенством, которое называют также уравнением возможных работ. Это равенство в аналитической форме имеет вид:

. (10.4)

Принцип возможных перемещений устанавливает общее условие равновесия механической системы, не требующеё рассмотрения равновесия отдельных частей (тел) этой системы и позволяющее при идеальных связях исключить из рассмотрения все заранее неизвестные реакции связей.

Для решения задач геометрическим методом, когда система имеет одну степень свободы, необходимо:

1) изобразить все действующие на систему активные силы;

2) сообщить системе возможное перемещение и показать на чертеже элементарные перемещения 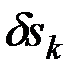точек приложения сил или углы элементарных поворотов тел, на которые действуют силы (у элементарных перемещений на чертеже указываются их модули 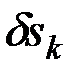, которые непосредственно входят в условия равновесия);

3) определить элементарные работы всех активных сил на данном перемещении по формулам:

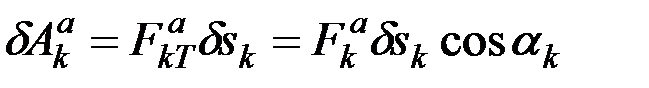
или

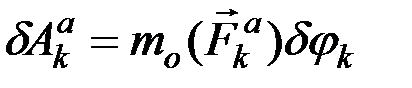
(10.5)

и составить условие (10.2);

4) установить зависимость между величинам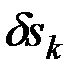и и , вошедшими в равенство (10.2), и выразить эти величины через какую-нибудь одну, что для системы с одной степенью свободы всегда можно сделать.

После замены в равенстве (10.2) всех величин 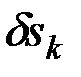, через одну получим уравнение, с помощью которого определяется искомая величина или зависимость.

Зависимости между 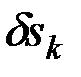и 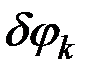можно находить:

а) из соответствующих геометрических соотношений;

б) из кинематических соотношений, считая, что система движется, и определяя при данном положении системы зависимости между линейными 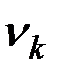или угловыми скоростями соответствующих точек или тел системы, а затем полагая 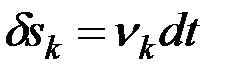, , что справедливо, так как получаемые точками или телами за время действительные перемещения будут при стационарных связях одними из возможных.

Для системы с несколькими степенями свободы задачу можно решить, составив условие для каждого из независимых возможных перемещений системы и преобразовав его тем же путем. В результате для системы получится столько условий равновесия, сколько степеней свободы она имеет.

При аналитическом методе расчёта условие равновесия составляют в виде равенства (10.4). Для этого выбирают координатные оси, связанные с телом, которое при возможных перемещениях системы остается неподвижным. Затем вычисляют проекции всех активных сил на выбранные оси и координаты , , 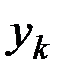точек приложения этих сил, выражая все координаты через какой-нибудь параметр (например, угол). После этого величины , , 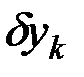находятся путём дифференцирования координат 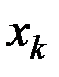, , 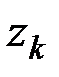по этому параметру.

Если все координаты 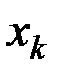, , 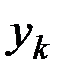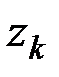выразить через один параметр сразу не удастся, то следует ввести несколько параметров, а затем установить зависимость между ними.

Отметим в заключение, что условиями выражений (10.2) или (10.4) можно пользоваться для решения задач и при наличии трения, включая силу трения в число активных сил. Этим же путем можно находить реакции связей, если, отбросив связь, заменить её соответствующей реакцией, включить последнюю в число активных сил и учесть, что после отбрасывания связи у системы появляется новая степень свободы.

Пример 7. Найти зависимость между моментом пары, действующим на кривошип кривошипно-ползунного механизма (рис. 37) и силой давления на поршень при равновесии, если , , .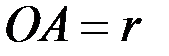

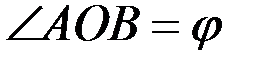Рис. 37

Решение. У механизма одна степень свободы. Из условия равновесия (10.2), если положить 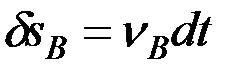, , 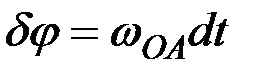получим

или .

Решение сводится к определению зависимости между 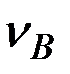и .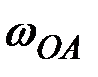

Рис. 38

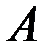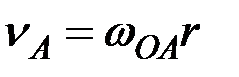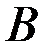Точка имеет скорость, численно равную и направленную перпендикулярно , а скорость точки направлена вдоль . Этих данных достаточно для определения всех кинематических характеристик шатуна .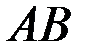

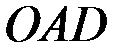По теореме о проекциях скоростей . Но поскольку угол (рис. 38), как внешний угол треугольника 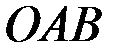, равен 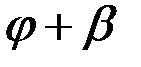, то 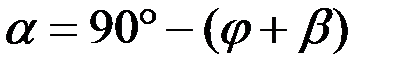и, следовательно

.

Исключим из этого равенства угол 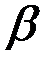. Из треугольника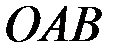 . Кроме того,

.

В результате находим

.

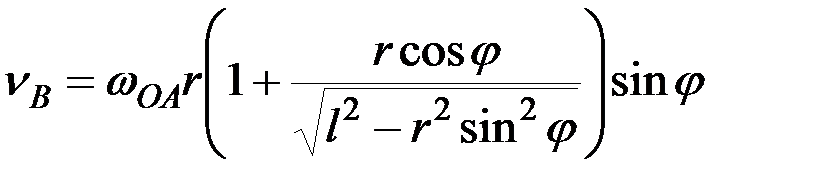Пользуясь полученным результатом, находим

.

Date: 2015-09-03; view: 766; Нарушение авторских прав