Обобщённые силы

Рассмотрим механическую систему, состоящую из материальных точек, на которые действуют силы . Пусть система имеет s степеней свободы, и её положение определяется обобщенными координатами. Сообщим системе такое независимое возможное перемещение, при котором координата получает приращение 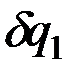, а остальные координаты не изменяются. Тогда каждый из радиус-векторов 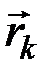точек системы получит элементарное приращение 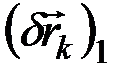. Поскольку, согласно равенству (12.1), 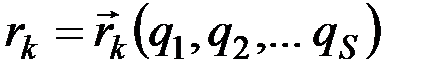, а при рассматриваемом перемещении изменяется только координата (остальные сохраняют постоянные значения), то 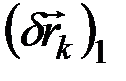вычисляются как частный дифференциал и, следовательно,

.

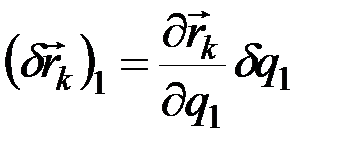Используя это равенство, вычислим сумму элементарных работ всех действующих сил на рассматриваемом перемещении, которую обозначим 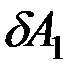. Получим

.

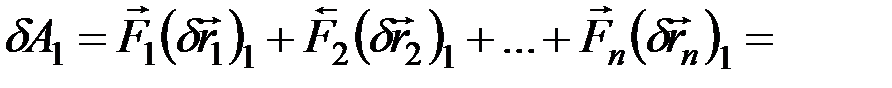
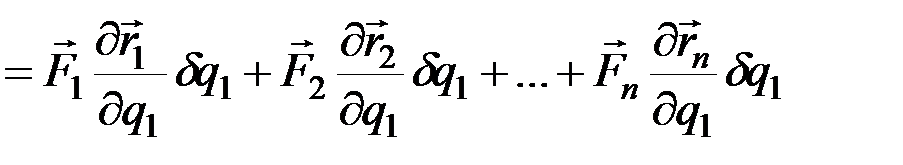Вынося общий множитель за скобки, найдём окончательно

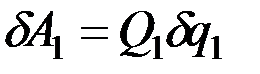, (12.3)

где обозначено

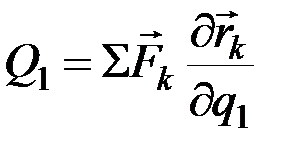. (12.4)

По аналогии с равенством 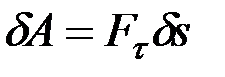, определяющим элементарную работу силы , величину 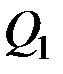называют обобщённой силой, соответствующей координате .

Сообщая системе другое независимое возможное перемещение, при котором изменяется только координата 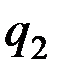, получим для элементарной работы всех действующих сил на этом перемещении выражение

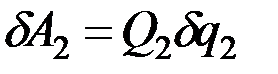, (12.5)

где

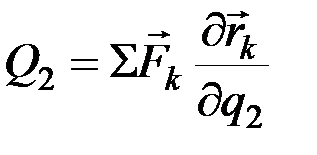. (12.6)

Величина 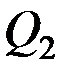представляет собой обобщённую силу, соответствующую координате и т.д.

Очевидно, что если системе сообщить такое возможное перемещение, при котором одновременно измеряются все её обобщённые координаты, то сумма элементарных работ приложенных сил на этом перемещении определится равенством:

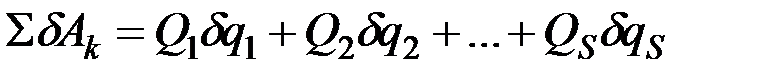. (12.7)

Формула (12.7) дает выражение полной элементарной работы всех действующих на систему сил в обобщённых координатах. Из этого равенства видно, что обобщённые силы – это величины, равные коэффициентам при приращениях обобщённых координат в выражении полной работы действующих на систему сил.

Если все наложенные на систему связи являются идеальными, то работу при возможных перемещениях совершают только активные силы и величины 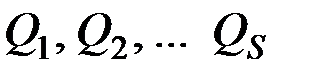будут представлять собой обобщённые активные силы системы.

Размерность обобщённой силы зависит от размерности соответствующей обобщённой координаты. Так как произведение 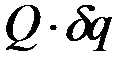, а следовательно и 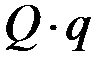имеет размерность работы, то

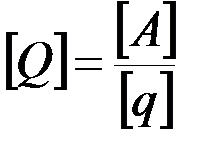, (12.8)

т.е. размерность обобщённой силы равна размерности работы, делённой на размерность соответствующей обобщённой координаты.

Отсюда видно, что если 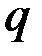– линейная величина, то 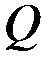имеет размерность обычной силы (в системе СИ измеряется в ньютонах); если 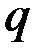– угол (величина безразмерная), то будет измеряться в 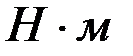(размерность момента); если 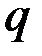– объём (например, положение поршня в цилиндре можно определять объёмом запоршневого пространства), то будет измеряться в 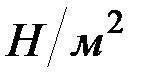(размерность давления) и т.д. Как видим, по аналогии с обобщенной скоростью, понятием об обобщенной силе охватываются все величины, встречающиеся ранее как меры механического взаимодействия материальных тел (сила, момент силы, давление).

Вычисление обобщённых сил будем производить по формулам (12.3), (12.5), что сводится к вычислению возможной элементарной работы. Сначала следует установить, каково число степеней свободы системы, выбрать обобщённые координаты и изобразить на чертеже все приложенные к системе активные силы и силы трения (если они совершают работу). Затем для определения 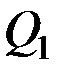необходимо сообщить системе такое возможное перемещение, при котором изменяется только координата ; получив положительное приращение 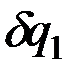, вычислить на этом перемещении сумму элементарных работ всех действующих сил по формулам (10.5) и представить полученное выражение в виде (12.3). Тогда коэффициент при 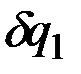и дает искомую величину 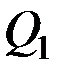. Аналогично вычисляются , …

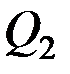Пример 9. Подсчитаем обобщённую силу для системы, изображённой на рис. 40, где груз А весом перемещается по гладкой наклонной поверхности, а груз В весом 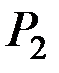– по шероховатой горизонтальной плоскости, коэффициент трения о которую равен .

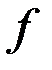Рис. 40

Решение. Грузы связаны нитью, перекинутой через блок О. Массой нити и блока пренебрегаем. Система имеет одну степень свободы, и её положение определяется координатой 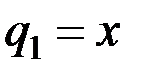(положительное направление отсчета 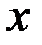показано стрелкой). Для определения 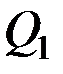сообщаем системе возможное перемещение 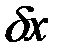, при котором , вычисляем на этом перемещении элементарные работы сил 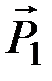и 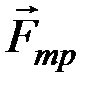; остальные силы работы не совершают. Так как 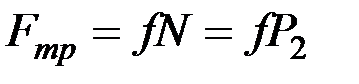, то

.

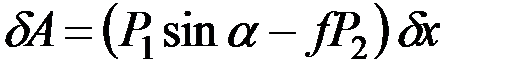Следовательно,

.

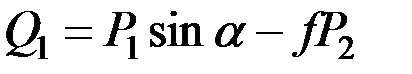Случай потенциальных сил. Если все действующие на систему силы являются потенциальными, то для системы, как известно, существует такая силовая функция U, зависящая от координат х_k, y_k, z_k точек системы, что сумма элементарных работ действующих сил равна полному дифференциалу этой функции, т. е. 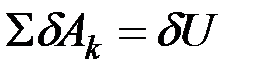. Но при переходе к обобщенным координатам 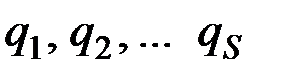все х_k, y_k, z_k могут быть выражены через эти координаты и тогда 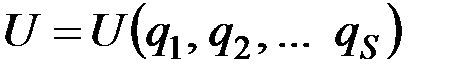. Следовательно, вычисляя как полный дифференциал от функции , найдём, что

.

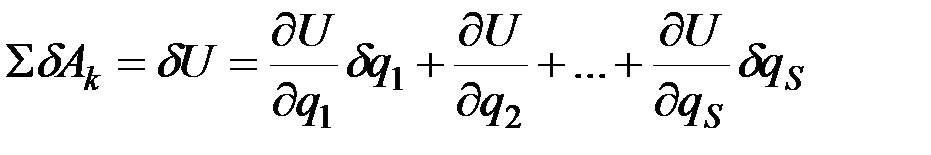Сравнивая это выражение с равенством (12.7), заключаем, что в данном случае

, (12.9)

или, так как потенциальная энергия 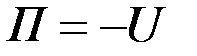, то

. (12.10)

Следовательно, если все действующие на систему силы потенциальны, то обобщённые силы равны частным производным от силовой функции (или взятым со знаком минус частным производным от потенциальной энергии) по соответствующим обобщенным координатам.

Date: 2015-09-03; view: 799; Нарушение авторских прав