Обобщённые координаты и обобщенные скорости

Число координат (параметров), определяющих положение механической системы, зависит от количества точек (или тел), входящих в систему, а также от числа и характера наложенных связей. В дальнейшем будем рассматривать только системы с геометрическими связями (точнее, только голономные системы). У такой системы число независимых координат, определяющих положение системы, совпадает с числом её степеней свободы. В качестве этих координат можно выбирать параметры, имеющие любую размерность и любой геометрический (или физический) смысл, в частности отрезки прямых или дуг, углы, площади и т.п.

Независимые друг от друга параметры любой размерности, число которых равно числу степени свободы системы и которые однозначно определяют её положение, называют обобщёнными координатами системы. Будем обозначать обобщенные координаты буквой q. Тогда положение системы, имеющей s степеней свободы, будет определяться s обобщенными координатами

.

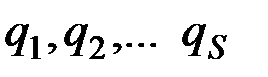Поскольку обобщённые координаты друг от друга независимы, то элементарные приращения этих координат

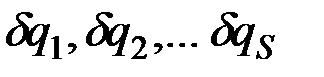
также независимы. При этом каждая из этих величин определяет соответствующее, независимое от других возможное перемещение системы.

Как при всяком переходе от одной системы координат к другой, декартовы координаты х_k, y_k, z_k любой точки рассматриваемой механической системы можно выразить через обобщенные координаты зависимости вида: и т. д. Следовательно, и для радиус-вектора этой точки, поскольку 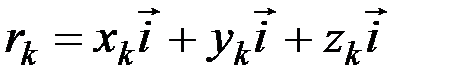, тоже будет

. (12.1)

При движении системы её обобщенные координаты будут с течением времени непрерывно изменяться, и закон этого движения определится уравнениями:

. (12.2)

Уравнения (12.2) представляют собой кинематические уравнения движения системы в обобщённых координатах.

Производные от обобщённых координат по времени называются обобщёнными скоростями системы. Обозначим обобщенные скорости символами

,

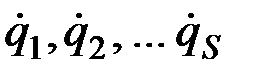где 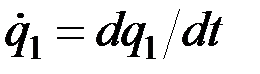и т.д. Размерность обобщённой скорости зависит от размерности соответствующей обобщённой координаты. Если 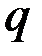– линейная величина, то – линейная скорость; если 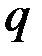– угол, то – угловая скорость; если 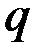– площадь, то 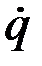– секторная скорость и т.д. Как видим, понятием обобщённой скорости охватываются все встречавшиеся нам ранее в кинематике понятия о скоростях.

Date: 2015-09-03; view: 932; Нарушение авторских прав