Принцип Даламбера для точки и механической системы

Методы решения задач механики, которые рассматривались выше, основываются на уравнениях, вытекающих или непосредственно из законов Ньютона, или же из общих теорем, являющихся следствием этих законов. Однако этот путь не является единственным. Оказывается, что уравнения движения или условия равновесия механической системы можно получить, положив в основу вместо законов Ньютона другие общие положения, называемые принципами механики. В ряде случаев применение этих принципов позволяет найти более эффективные методы решения соответствующих задач.

Найдём сначала выражение принципа для одной материальной точки. Пусть на материальную точку массой действует система активных сил, равнодействующую которых обозначим 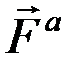, и реакция связи 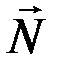(если точка является несвободной). Под действием всех сил точка будет двигаться по отношению к инерциальной системе отсчёта с некоторым ускорением .

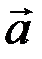Введём в рассмотрение величину

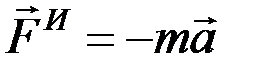, (9.1)

имеющую размерность силы.

Векторную величину, равную по модулю произведению массы точки на её ускорение и направленную противоположно этому ускорению, называют силой инерции точки.

Тогда оказывается, что движение точки обладает следующим свойством: если в любой момент времени к действующим на точку активным силам и реакции связи присоединить силу инерции, то полученная сила будет уравновешенной, т. е.

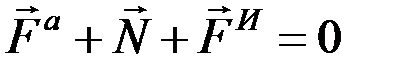. (9.2)

Это положение выражает принцип Даламбера для материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона для рассматриваемой точки:

.

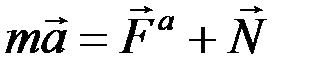Перенося здесь величину в правую часть равновесия и учитывая выражение (9.1), придём к соотношению (9.2). Наоборот, перенося в уравнении (9.2) величину в другую часть равновесия и учитывая выражение (9.1), получим выражение второго закона Ньютона.

Рассмотрим теперь механическую систему, состоящую из 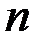материальных точек. Выделим какую-нибудь из точек системы массой 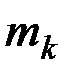. Под действием приложенных к ней внешних и внутренних сил и 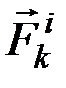(в которые входят и активные силы, и реакции связей) точка будет двигаться по отношению к инерциальной системе отсчёта с некоторым ускорением . Введя для этой точки силу инерции 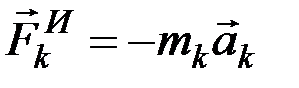, получим

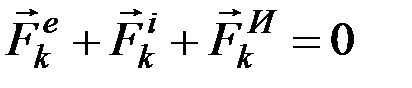, (9.3)

т.е. что 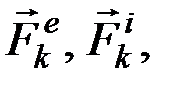и 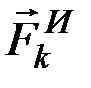образуют уравновешенную систему сил. Рассуждая аналогично для каждой из точек системы, приходим к результату, выражающему принцип Даламбера для системы: если в любой момент времени к каждой из точек систем, кроме действующих на неё внешних и внутренних сил, присоединить соответствующие силы инерции, то полученная система сил будет уравновешенной и к ней можно применять все уравнения статики.

Математически принцип Даламбера для механической системы выражается векторными равенствами вида (9.3), которые, очевидно, эквивалентны дифференциальным уравнениям движения системы. Следовательно, из принципа Даламбера, можно получить все общие теоремы динамики.

Значение принципа Даламбера состоит в том, что при непосредственном его применении к задачам динамики уравнения движения системы составляются в форме хорошо известных уравнений равновесия, – это делает единообразным подход к решению задач и часто упрощает соответствующие расчёты.

Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую механическую систему. Тогда на основании принципа Даламбера должно быть:

;

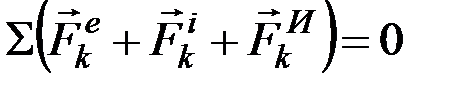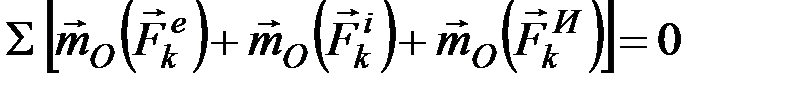. (9.4)

Введём обозначения:

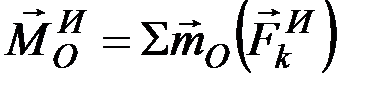, . (9.5)

Величина 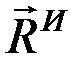, представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, подставляя выражение (9.5) в выражение (9.4) и учитывая, что геометрическая сумма внутренних сил и их моментов равны нулю, получим:

,

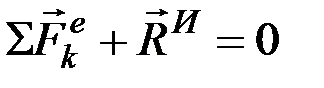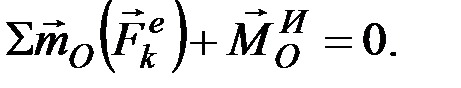(9.6)

Применение уравнений (9.6), вытекающих из принципа Даламбера, упрощает процесс решения задач, так как эти уравнения не содержат внутренних сил. По существу эти уравнения эквивалентны уравнениям, выражающим теоремы об изменении количества движения и главного момента количеств движения системы, и отличаются от них только по форме.

Уравнениями (9.6) особенно удобно пользоваться при изучении движения твёрдого тела или систем твёрдых тел.

В проекциях на координатные оси равенства (9.6) дают уравнения, аналогичные соответствующим уравнениям статики. Чтобы пользоваться этими уравнениями при решении задач, необходимо знать выражения главного вектора и главного момента сил инерций.

Date: 2015-09-03; view: 787; Нарушение авторских прав