Физический маятник

Физическим маятником называется твердое тело, имеющее неподвижную горизонтальную ось вращения, не проходящую через его центр тяжести, и находящееся под действием только силы тяжести.

Рис. 33

Изобразим сечение маятника плоскостью, перпендикулярной оси подвеса и проходящей через центр масс маятника 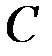(рис. 33, а).

Введём обозначения: 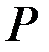– вес маятника, 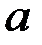– расстояние от центра масс до оси подвеса, 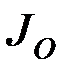– момент инерции маятника относительно оси подвеса. Положение маятника будем определять углом 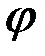отклонения линии 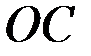от вертикали.

Для определения закона колебаний маятника воспользуемся дифференциальным уравнением вращательного движения.

В данном случае

,

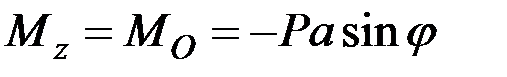(знак «–» взят потому, что при момент отрицателен, а при – положителен), уравнение движения принимает вид:

. (8.31)

Поделив обе части равенства на 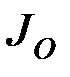и введя обозначение

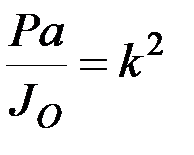, (8.32)

найдём дифференциальное уравнение колебаний маятника в виде:

. (8.33)

Полученное дифференциальное уравнение в обычных функциях не интегрируется. Ограничимся рассмотрением малых колебаний маятника, считая приближенно (это можно сделать, когда угол много меньше одного радиана). Тогда будем иметь

. (8.34)

Это дифференциальное уравнение совпадает по виду с дифференциальным уравнением свободных прямолинейных колебаний точки, и его общее решение по аналогии с равенством (3.3) имеет вид:

. (8.35)

Полагая, что в начальный момент маятник отклонён на малый угол 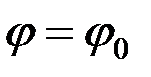и отпущен без начальной скорости , найдём для постоянных интегрирования значения: 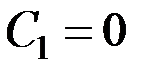, . Тогда закон малых колебаний маятника при данных начальных условиях будет иметь вид:

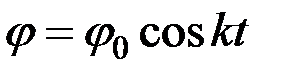. (8.36)

Следовательно, малые колебания физического маятника являются гармоническими. Период малых колебаний физического маятника, если заменить 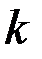его значением, определяется формулой:

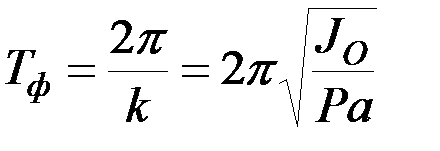. (8.37)

Как видим, для малых колебаний период от угла начального отклонения 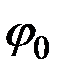не зависит. Этот результат является приближенным. Если проинтегрировать составленное вначале дифференциальное уравнение колебаний маятника, не считая в нём угол 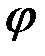малым (т. е. не полагая 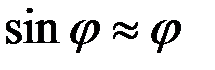), то можно убедиться, что зависит от 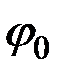. Приближенно эта зависимость имеет вид

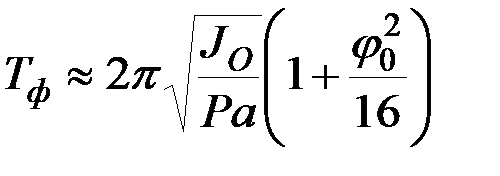. (8.38)

Отсюда, например, следует, что при 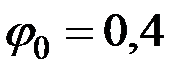радиана (около 23°) формула (8.38) определяет период с точностью до 1%.

Полученные результаты охватывают и случай так называемого математического маятника, т.е. груза малых размеров (который будем рассматривать как материальную точку), подвешенного на нерастяжимой нити длиной 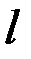, массой которой, по сравнению с массой груза, можно пренебречь (рис. 33, б). Для математического маятника, так как он представляет собой систему, состоящую из одной материальной точки, очевидно, что

, .

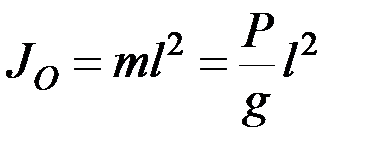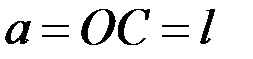Подставив эти величины в равенство (8.38), найдём, что период малых колебаний математического маятника определяется формулой

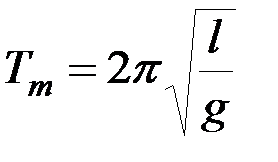. (8.39)

Из сравнения формул (8.37) и (8.39) видно, что при длине

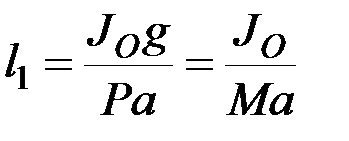(8.40)

период колебаний математического маятника совпадает с периодом колебаний соответствующего физического маятника.

Длина такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника, называется приведённой длиной физического маятника. Точка 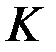, отстоящая от оси подвеса на расстоянии 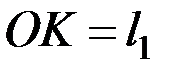называется центром качаний физического маятника (рис. 33, а).

Замечая, что, по теореме Гюйгенса

,

мы можем привести формулу (8.40) к виду:

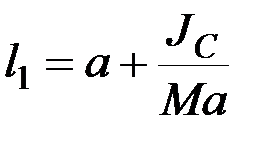. (8.41)

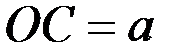Отсюда следует, что расстояние всегда больше, чем ,т. е. что центр качаний физического маятника всегда расположен ниже его центра масс.

Один из экспериментальных методов определения моментов инерции тел (метод маятниковых колебаний) основан на использовании формулы (8.37) периода малых колебаний маятника.

Контрольные вопросы

1. Как определяется импульс переменной силы за конечный промежуток времени? Что характеризует импульс силы?

2. Чему равны проекции импульса постоянной и переменной силы на оси координат?

3. Как изменяется количество движения точки, движущейся равномерно по окружности?

4. Чему равен импульс равнодействующей?

5. Что называется количеством движения механической системы?

6. В чём состоит теорема об изменении количества движения (для точки и для системы)?

7. При каких условиях количество движения механической системы не изменяется? При каких условиях не изменяется его проекция на некоторую ось?

8. Что называется моментом количества движения материальной точки?

9. В чём состоит теорема об изменении момента количества движения точки?

10. Как определяется работа постоянной по модулю и направлению силы на прямолинейном перемещении?

11. Каким простым способом можно вычислить работу постоянной по модулю и направлению силы на криволинейном перемещении?

12. Чему равна работа равнодействующей силы?

13. Дайте формулировку теоремы об изменении кинетической энергии материальной точки.

14. Как вычисляется кинетическая энергия твёрдого тела в различных случаях его движения?

15. Сформулируйте теорему об изменении кинетической энергии механической системы.

16. Что называют приведённой длиной, центром и осью качания физического маятника?

17. По какой формуле вычисляется приведённая длина физического маятника?

18. По какой формуле вычисляется период малых колебаний физического маятника?

19. Назовите способы опытного определения моментов инерции твёрдых тел.

Date: 2015-09-03; view: 736; Нарушение авторских прав