Кинетическая энергия твёрдого тела

Поступательное движение твёрдого тела. При поступательном движении твёрдого тела скорости всех его точек в каждый момент времени геометрически равны между собой (рис. 27).

Рис. 27

Кинетическая энергия тела определяется уравнением:

.

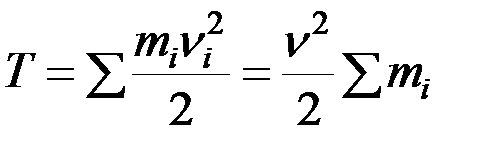Так как 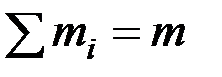, то окончательно

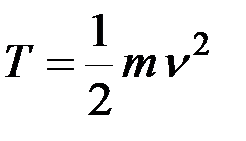. (8.24)

На основании выражения (8.24) устанавливаем, что кинетическом энергия твёрдого тела, движущегося поступательно, равна половине произведения массы тела на квадрат его скорости.

Таким образом, кинетическая энергия тела, движущегося поступательно, вычисляется как кинетическая энергия материальной точки, имеющей массу этого тела.

Вращение твёрдого тела вокруг неподвижной оси. При вращении твёрдого тела вокруг неподвижной оси (рис. 28) скорость любой точки тела определяется как вращательная скорость:

.

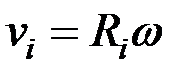Рис. 28

Кинетическую энергию твёрдого тела определяем по формуле:

.

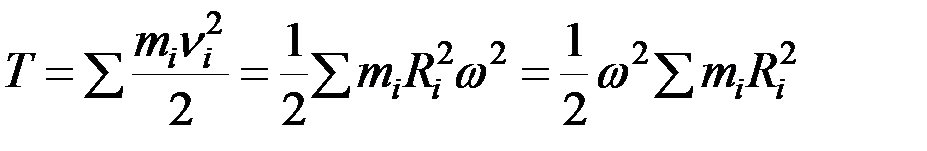Здесь 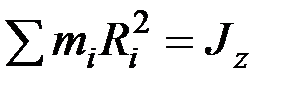– момент инерции тела относительно оси вращения.

Кинетическая энергия тела равна

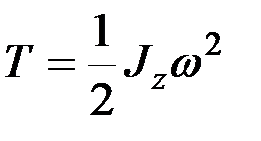. (8.25)

На основании выражения (8.25) устанавливаем, что кинетическая энергия твёрдого тела, вращающегося вокруг неподвижной оси, равна половине произведения его момента инерции относительно оси вращения на квадрат угловой скорости тела.

Сравнив формулы (8.24) и (8.25), можно заметить, что при вращении тела его момент инерции играет такую же роль, что и его масса при поступательном движении.

Плоское движение твёрдого тела. Предположим, что при плоском движении твёрдого тела его центр масс 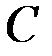движется в плоскости чертежа (рис. 29). Разложим это движение на поступательное движение вместе с центром масс и относительное движение по отношению к центру масс.

Рис. 29

В этом случае относительное движение представляет собой вращение тела вокруг оси, проходящей через центр масс 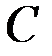перпендикулярно плоскости чертежа. Определим кинетическую энергию тела по теореме Кенига:

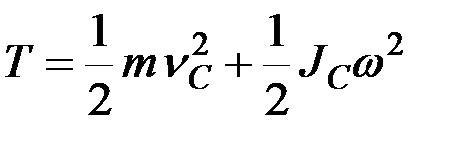. (8.26)

Здесь – кинетическая энергия тела в поступательном движении вместе с центром масс, а 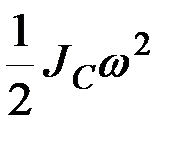– кинетическая энергия во вращении тела вокруг подвижной оси, определенная на основании формулы (8.25).

Сферическое движение твёрдого тела. Скорости точек твёрдого тела при сферическом движении в каждый момент можно рассматривать как вращательные вокруг мгновенной оси вращения (рис. 30).

Рис. 30

Поэтому кинетическая энергия тела, совершающего сферическое движение в данный момент, определяется по формуле

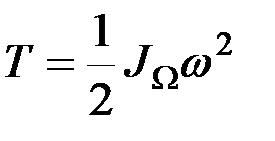, (8.27)

где – мгновенная угловая скорость тела; 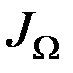– момент инерции твёрдого тела относительно мгновенной оси вращения.

Выражение (8.27) показывает, что кинетическая энергия твёрдого тела, совершающего сферическое движение, равна половине произведения момента инерции тела относительно мгновенной оси вращения на квадрат угловой скорости тела.

При этом значение момента инерции 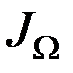непрерывно изменяется, так как изменяется положение мгновенной оси относительно тела.

Общий случай движения твёрдого тела. Движение свободного твёрдого тела в общем случае можно разложить на два составляющих движения: на переносное поступательное движение вместе с центром масс и относительное сферическое движение относительно центра масс (рис. 31).

Рис. 31

Тогда кинетическая энергия тела определяется по формуле:

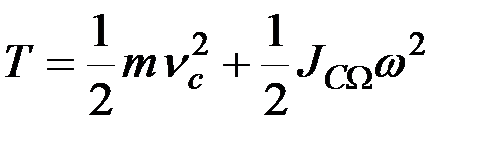. (8.28)

Таким образом, кинетическая энергия твёрдого тела в общем случае его движения равна сумме кинетической энергии тела в его переносном поступательном движении вместе с центром масс и его кинетической энергии в сферическом движении относительно центра масс.

Date: 2015-09-03; view: 1102; Нарушение авторских прав