Теорема об изменении момента количества движения материальной точки

Предположим, что движение материальной точки происходит под действием силы 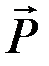(рис. 25).

Рис. 25

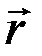Проведём из произвольного центра в точку радиус-вектор и определим момент силы 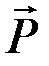относительно этого центра по формуле из статики:

.

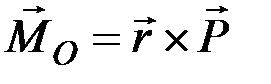Определим также момент количества движения точки относительно центра по формуле (8.16):

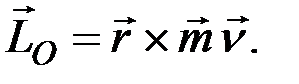
Чтобы установить зависимость между моментом количества движения точки 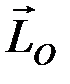и моментом силы 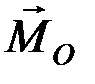,следует найти производную по времени от момента количества движения:

.

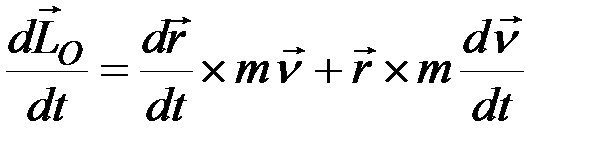Здесь

,

.

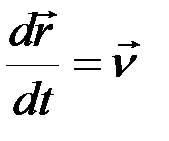Пользуясь этими выражениями, получаем

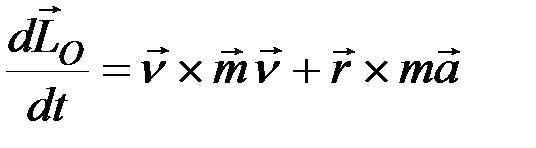. (8.20)

Так как угол (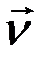, 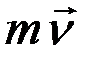) = 0, то

,

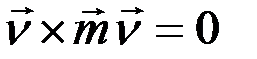тогда

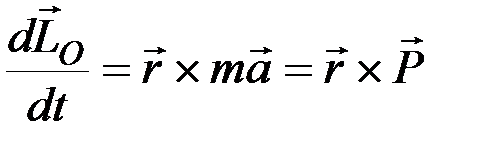
или

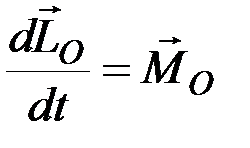. (8.21)

Если на материальную точку действует несколько сил, то 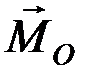следует рассматривать как момент их равнодействующей. Заменим геометрической суммой моментов составляющих сил:

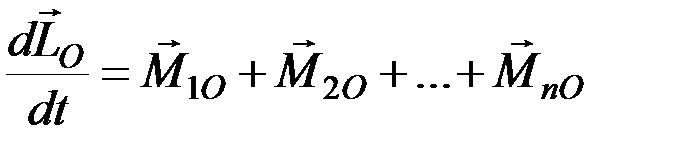
или

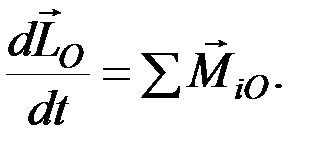(8.22)

Соотношение (8.22) выражает теорему об изменении момента количества движения материальной точки относительно центра: производная по времени от момента количества движения материальной точки относительно некоторого неподвижного центра равна геометрической сумме моментов сил, действующих на точку, относительно того же центра.

Так как проекция векторной производной на любую ось равна производной от её проекции на эту ось, то, проецируя векторное равенство (8.22) на оси 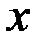, , , 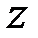получим три равенства:

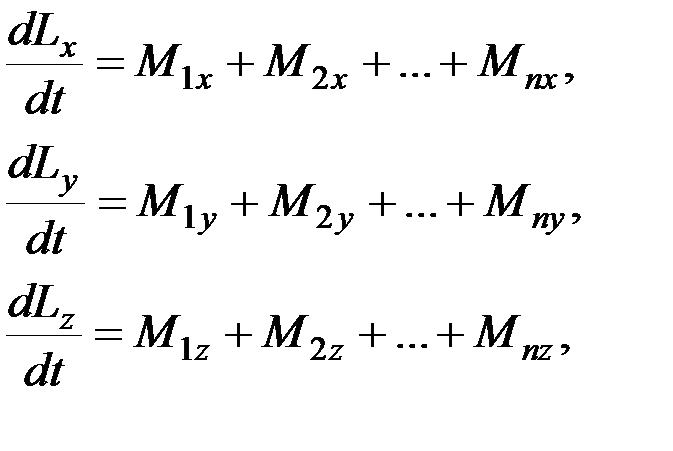
или

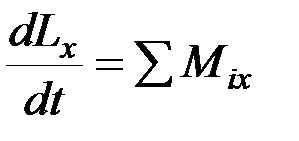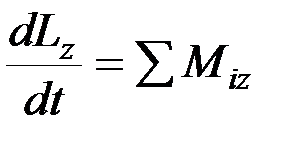, , . (8.23)

Здесь, согласно уравнению (8.19), 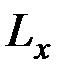, , 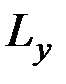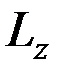– моменты количества движения точки относительно осей координат, a , , 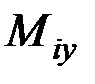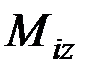– моменты силы 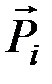относительно этих же осей.

Равенства (8.23) выражают теорему об изменении момента количества движения точки относительно оси: производная по времени от момента количества движения материальной точки относительно некоторой неподвижной оси равна алгебраической сумме моментов сил, действующих на точку, относительно этой же оси.

Пример 3. Шарик весом 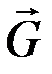находится на гладкой горизонтальной плоскости. К шарику привязывают невесомую нерастяжимую нить, которую пропускают через отверстие на плоскости и тянут вниз с постоянной скоростью (рис. 26, а).

Рис. 26

В момент, когда расстояние шарика ототверстия ОМ ₀= R, шарику сообщают скорость , направленную перпендикулярно нити ОМ ₀. Определить дальнейшее движение шарика.

Решение. Положение шарика 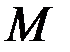на плоскости будем определять двумя полярными координатам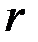и и 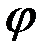. Проведем ось 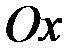через начальное положение шарика 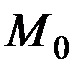. Тогда начальные условия будут 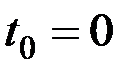, , 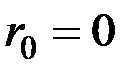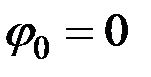(рис. 26, б).

На шарик действуют три силы: сила веса 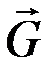, реакция плоскости 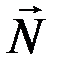и реакция нити 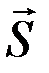.Так как момент каждой из этих сил относительно вертикальной оси 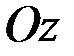равен нулю, то

.

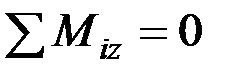Согласно уравнению (8.23),

.

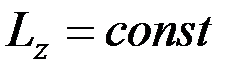Так как по условию задачи нить втягивается равномерно со скоростью 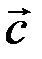,то изменение координаты определится уравнением

.

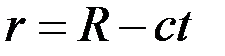Для определения координаты r в зависимости от t воспользуемся условием L_z = const. Абсолютная скорость шарика состоит из двух скоростей, направленных вдоль осей полярной системы координат: скорости 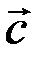и перпендикулярной ей скорости 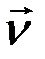, модуль которой равен

.

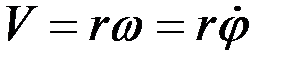Вектор количества движения не имеет момента относительно оси 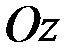, так как прямая, по которой он направлен, пересекает ось .

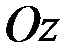Момент вектора количества движения 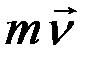относительно оси 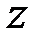в любой момент времени определяется по формуле (8.17):

.

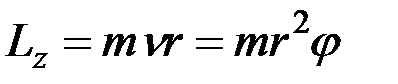В начальный момент .

Так как L= const, то ,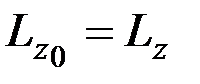

т.е.

,

откуда

,

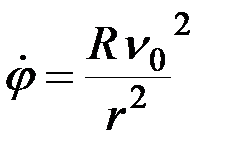или после подстановки значения :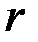

.

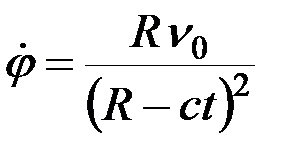Проинтегрируем это выражение по времени:

.

Постоянную определим путём подстановки в уравнение начальных условий , :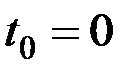

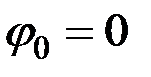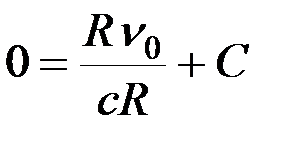, откуда .

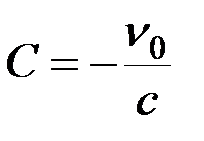Подставив значение С, получим второе уравнение движения шарика:

.

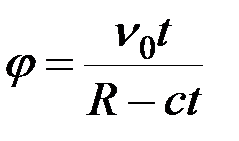Уравнение траектории шарика в полярных координатах, полученное исключением t из его уравнений движения имеет вид:

.

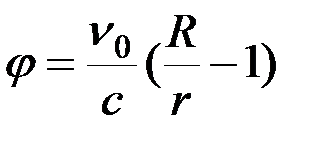Отметим, как это следует из выражения

,

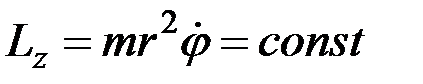что при уменьшении величины r возрастает угловая скорость вращения нити .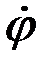

Date: 2015-09-03; view: 672; Нарушение авторских прав