
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Производная. Ее физический и геометрический
|
|
смысл
Пусть функция  определена на интервале
определена на интервале  . Возьмем какое-либо значение
. Возьмем какое-либо значение 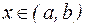 и дадим аргументу x произвольное приращение
и дадим аргументу x произвольное приращение  , такое, что
, такое, что 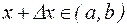 .
.
Назовем приращением функции 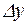 величину
величину 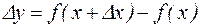 .
.
Мы уже раньше выяснили, что если при 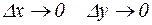 , то функция
, то функция 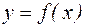 непрерывна в точке х:
непрерывна в точке х:
если 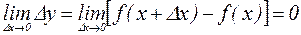 , то функция непрерывна. Будем считать функцию непрерывной.
, то функция непрерывна. Будем считать функцию непрерывной.
Будем также считать, что 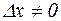 и составим отношение
и составим отношение  .
.
Т.к. величина аргумента x фиксирована, а 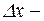 произвольное приращение аргумента, то отношение
произвольное приращение аргумента, то отношение 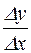 представляет собой функцию от
представляет собой функцию от  . Это отношение определено при небольших
. Это отношение определено при небольших  (в окрестности точки
(в окрестности точки 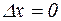 ) за исключением точки
) за исключением точки 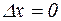 . Мы имеем право рассматривать вопрос о существовании предела этого отношения при
. Мы имеем право рассматривать вопрос о существовании предела этого отношения при 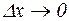 .
.
Определение.
Производной функции 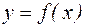 в точке х называется предел (если он существует) отношения приращения функции к приращению аргумента, когда последний стремится к нулю.
в точке х называется предел (если он существует) отношения приращения функции к приращению аргумента, когда последний стремится к нулю.
Обозначение:  .
.
Отметим, что если 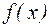 определена на
определена на  и если при всех
и если при всех 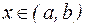 имеется производная, то эта производная является функцией
имеется производная, то эта производная является функцией 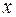 и эта функция
и эта функция 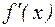 также определена на интервале
также определена на интервале  .
.
Физический смысл производной
Пусть функция 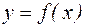 описывает закон движения точки по прямой линии, причем х представляет собой время, а у – путь, пройденный за это время точкой от начала отсчета пути. Тогда
описывает закон движения точки по прямой линии, причем х представляет собой время, а у – путь, пройденный за это время точкой от начала отсчета пути. Тогда 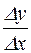 – средняя скорость движения за промежуток времени от х до
– средняя скорость движения за промежуток времени от х до 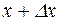 , а
, а 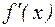 – мгновенная скорость в момент времени х. В этом и заключается физический смысл производной (точнее говоря, механический).
– мгновенная скорость в момент времени х. В этом и заключается физический смысл производной (точнее говоря, механический).
Точно так же можно считать, что х – время, а функция 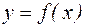 определяет количество электричества, прошедшее через поперечное сечение некоторого проводника за время х. В этом случае
определяет количество электричества, прошедшее через поперечное сечение некоторого проводника за время х. В этом случае  определяет скорость изменения во времени количества электричества, т.е. представляет собой силу тока в проводнике в момент времени х.
определяет скорость изменения во времени количества электричества, т.е. представляет собой силу тока в проводнике в момент времени х.
Геометрический смысл производной
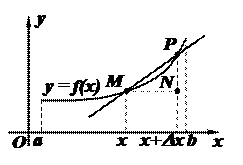 Рассмотрим график функции
Рассмотрим график функции 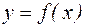 на интервале
на интервале  . Пусть
. Пусть 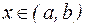 , а
, а  – произвольное приращение аргумента. Пусть М и Р – точки графика, соответствующие значениям аргумента х и
– произвольное приращение аргумента. Пусть М и Р – точки графика, соответствующие значениям аргумента х и 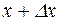 .
.
Проведем 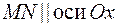 ,
, 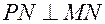 . Тогда
. Тогда 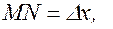
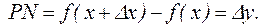 Проведем секущую MP. Обозначим угол ее наклона к оси x
Проведем секущую MP. Обозначим угол ее наклона к оси x 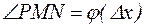 .
.
Тогда, очевидно,  . (*)
. (*)
Теперь устремим  к нулю. Очевидно, точка Р на графике будет приближаться к точке М, а секущая МР будет поворачиваться относительно точки М. При этом угол
к нулю. Очевидно, точка Р на графике будет приближаться к точке М, а секущая МР будет поворачиваться относительно точки М. При этом угол 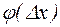 будет изменяться. Поскольку в равенстве (*) правая часть имеет предел при
будет изменяться. Поскольку в равенстве (*) правая часть имеет предел при 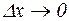 , равный значению производной
, равный значению производной 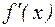 , это означает, что существует предельное значение угла
, это означает, что существует предельное значение угла 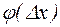 при
при 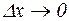 . В этом случае говорят, что график
. В этом случае говорят, что график 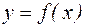 имеет в точке x касательную, тангенс угла наклона этой касательной к оси Ох равен производной в точке х. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом этой прямой. Таким образом, геометрический смысл производной состоит в следующем: производная
имеет в точке x касательную, тангенс угла наклона этой касательной к оси Ох равен производной в точке х. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом этой прямой. Таким образом, геометрический смысл производной состоит в следующем: производная 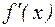 равна угловому коэффициенту касательной к графику функции в точке х.
равна угловому коэффициенту касательной к графику функции в точке х.
Понятие правой и левой производной
Определение.
Правой(левой) производной функции 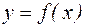 в точке х называется
в точке х называется 
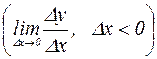 .
.
Обозначается:  правая,
правая, 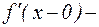 левая произ-водные.
левая произ-водные.
Если функция 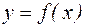 имеет в точке х производную, то она имеет в этой точке и левую и правую производные, причем они совпадают. Если функция
имеет в точке х производную, то она имеет в этой точке и левую и правую производные, причем они совпадают. Если функция 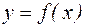 имеет в точке х и правую и левую производные, и они совпадают, то функция
имеет в точке х и правую и левую производные, и они совпадают, то функция 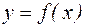 имеет в этой точке производную.
имеет в этой точке производную.
Пример функции, имеющей левую и правую производную, но не имеющей производной.
Пусть 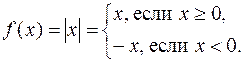
Правая производная 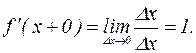
Левая производная 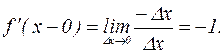
Производной нет, т.к. нет касательной!
График:
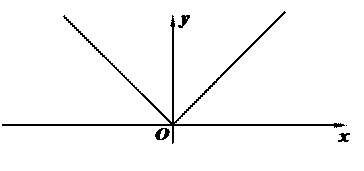 |
Теорема о непрерывности функции, имеющей производ-
ную
Если функция f имеет производную в точке х, то она непрерывна в этой точке.
Доказательство.
Из существования предела 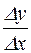 при
при 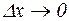 следует, что
следует, что  , где
, где 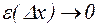 при
при 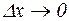 . Отсюда
. Отсюда 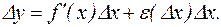
Перейдем к пределу при 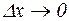 .
.
 Это и означает непрерывность функции.
Это и означает непрерывность функции.
Обратное утверждение, вообще говоря, не верно.
Непрерывная функция может не иметь производной. Пример мы уже имели: 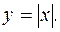
 |
В точке х=0 функция непрерывна, но произ-водной не имеет.
Date: 2015-09-02; view: 406; Нарушение авторских прав