
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Одновременное приведение двух квадратичных форм к сумме квадратов в линейном пространстве
|
|
Теорема 4.11 Пусть 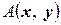 и
и  – симметричные билинейные формы, определенные в вещественном линейном пространстве V. Допустим далее, что для всех
– симметричные билинейные формы, определенные в вещественном линейном пространстве V. Допустим далее, что для всех 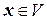 ,
,  , справедливо неравенство
, справедливо неравенство 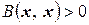 (т.е. квадратичная форма
(т.е. квадратичная форма  – положительно определенная). Тогда в пространстве V можно указать базис
– положительно определенная). Тогда в пространстве V можно указать базис 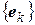 такой, что квадратичные формы
такой, что квадратичные формы  и
и  могут быть представлены в виде
могут быть представлены в виде
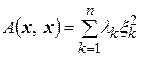 , (4.42)
, (4.42)
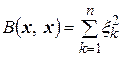 , (4.43)
, (4.43)
где 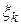 – координаты вектора
– координаты вектора  в базисе
в базисе 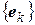 .
.
Алгоритм приведения пары квадратичных форм одним преобразованием одну к каноническому виду, а другую – к нормальному
1. Находим матрицы  и
и 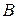 квадратичных форм
квадратичных форм 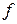 и
и  соответственно и определяем решения
соответственно и определяем решения  уравнения
уравнения  . Тогда канонический вид квадратичной формы
. Тогда канонический вид квадратичной формы 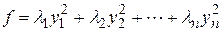 , а нормальный вид квадратичной формы
, а нормальный вид квадратичной формы 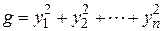 .
.
2. Найдем базисные векторы из системы уравнений  для каждого
для каждого  .
.
3. По матрице 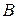 строим поляризацию
строим поляризацию 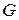 квадратичной формы
квадратичной формы  . Симметрическая билинейная функция
. Симметрическая билинейная функция 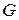 определяет скалярное произведение. К полученным базисным векторам применяется процесс ортогонализации Грамма-Шмидта относительно этого скалярного произведения.
определяет скалярное произведение. К полученным базисным векторам применяется процесс ортогонализации Грамма-Шмидта относительно этого скалярного произведения.
4. Составляем матрицу перехода из координат ортонормированных векторов и получаем формулы замены координат.
Пример 10 Для квадратичных форм 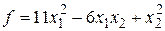 и
и 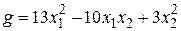 определить базис, в котором одна из этих квадратичных форм имеет канонический вид, а другая квадратичная форма приводится к нормальному виду, и соответствующую замену координат.
определить базис, в котором одна из этих квадратичных форм имеет канонический вид, а другая квадратичная форма приводится к нормальному виду, и соответствующую замену координат.
Решение. Находим матрицы  и
и 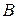 квадратичных форм
квадратичных форм 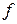 и
и  соответственно:
соответственно:
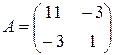 ,
, 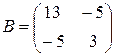 .
.
Форма 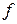 является положительно определенной, так как главные миноры ее матрицы положительны.
является положительно определенной, так как главные миноры ее матрицы положительны.
Решим уравнение 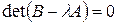 :
:
 ,
,
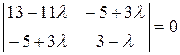 ,
,
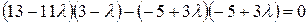 ,
, 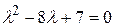 ,
, 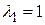 ,
,  .
.
Тогда канонический вид квадратичной формы 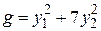 , а нормальный вид квадратичной формы
, а нормальный вид квадратичной формы 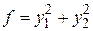 .
.
Для каждого из чисел 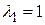 ,
,  решим матричное уравнение
решим матричное уравнение  .
.
При 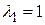 получаем
получаем 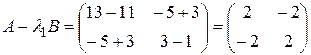 ,
,

При  получим
получим  . Тогда первый базисный вектор имеет вид
. Тогда первый базисный вектор имеет вид 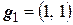 .
.
При  получаем
получаем 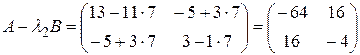 ,
,

При  получим
получим  . Тогда второй базисный вектор имеет вид
. Тогда второй базисный вектор имеет вид 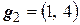 .
.
По матрице 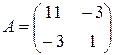 строим поляризацию
строим поляризацию 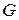 квадратичной формы
квадратичной формы  . Пусть
. Пусть 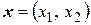 и
и 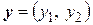 :
:
 .
.
Симметрическая билинейная функция 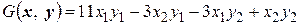 задает скалярное произведение. Векторы
задает скалярное произведение. Векторы 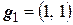 и
и 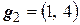 ортогональны относительно этого скалярного произведения:
ортогональны относительно этого скалярного произведения: 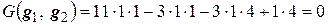 . Тогда векторы
. Тогда векторы  и
и 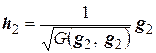 образуют ортонормированный базис относительно скалярного произведения, определяемого функцией
образуют ортонормированный базис относительно скалярного произведения, определяемого функцией 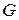 .
.
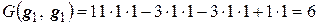 ,
,
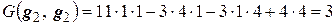 ,
,
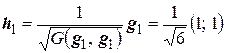 ,
,
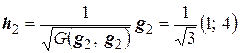 .
.
Тогда 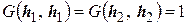 ,
, 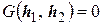 .
.
Запишем координаты векторов  и
и 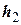 в виде столбцов матрицы. Получим матрицу перехода:
в виде столбцов матрицы. Получим матрицу перехода:
 .
.
Отсюда получаем замену переменных:
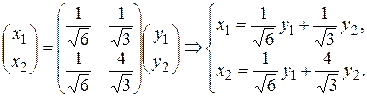
Date: 2015-08-24; view: 10895; Нарушение авторских прав