
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Билинейныеформы
|
|
Числовая функция  , аргументами которой являются всевозможные векторы
, аргументами которой являются всевозможные векторы  и
и  вещественного линейного пространства
вещественного линейного пространства  , называется билинейной формой, если для любых векторов
, называется билинейной формой, если для любых векторов  ,
,  ,
, 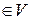 и любого вещественного числа λ выполняются соотношения
и любого вещественного числа λ выполняются соотношения
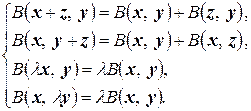 (4.1)
(4.1)
Иными словами, билинейная форма представляет собой числовую функцию  двух векторных аргументов
двух векторных аргументов  и
и  , определенную на всевозможных векторах
, определенную на всевозможных векторах  и
и  вещественного линейного пространства
вещественного линейного пространства  и линейную по каждому из этих аргументов.
и линейную по каждому из этих аргументов.
Пример 1 Скалярное произведение в евклидовом пространстве – пример билинейной функции.
Пример 2 Рассмотрим линейное пространство 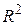 . Пусть
. Пусть  ,
, 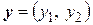 . Определим функцию
. Определим функцию  следующим образом:
следующим образом: 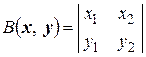 . Убедимся, что
. Убедимся, что  является билинейной функцией.
является билинейной функцией.
Пусть 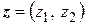 – вектор пространства
– вектор пространства 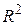 . Так как
. Так как 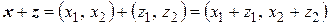 , то
, то
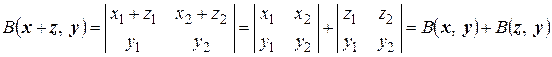 .
.
Так как 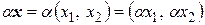 , то
, то
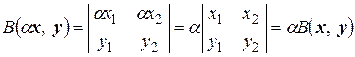 .
.
Так как 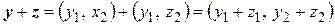 , то
, то
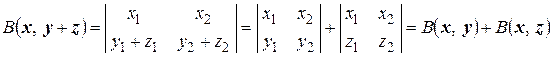 .
.
Так как 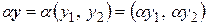 , то
, то
 .
.
Билинейная форма  называется симметричной (кососимметричной), если для любых векторов
называется симметричной (кососимметричной), если для любых векторов  и
и  линейного пространства
линейного пространства  выполняются соотношения
выполняются соотношения
 (
(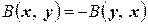 ). (4.2)
). (4.2)
Справедливо следующее утверждение: любую билинейную форму можно представить в виде суммы симметричной и кососимметричной билинейных форм.
Пусть в n -мерном линейном пространстве  задана билинейная форма
задана билинейная форма  . Выясним вопрос о представлении формы
. Выясним вопрос о представлении формы  в случае, когда в
в случае, когда в  задан определенный базис
задан определенный базис 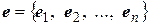 .
.
Справедливо следующее утверждение.
Теорема 4.1 Билинейная форма  при заданном в n-мерном линейном пространстве базисе
при заданном в n-мерном линейном пространстве базисе 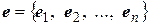 может быть однозначно представлена в следующем виде:
может быть однозначно представлена в следующем виде:
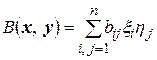 , (4.3)
, (4.3)
где
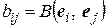 , (4.4)
, (4.4)
а 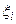 и
и 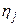 – координаты в базисе
– координаты в базисе 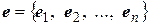 векторов
векторов  и
и  соответственно.
соответственно.
Матрица
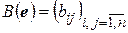 , (4.5)
, (4.5)
элементы 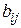 которой определены с помощью соотношений (4.4), называется матрицей билинейной формы
которой определены с помощью соотношений (4.4), называется матрицей билинейной формы  в данном базисе
в данном базисе 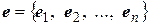 .
.
Замечание 1 Любая квадратная матрица 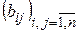 является в данном базисе
является в данном базисе 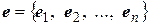 матрицей некоторой билинейной формы.
матрицей некоторой билинейной формы.
Замечание 2 Если  – симметричная (кососимметричная) билинейная форма, то матрица (4.5) этой формы в базисе е является симметричной (кососимметричной). Справедливо и обратное – если матрица (4.5) билинейной формы
– симметричная (кососимметричная) билинейная форма, то матрица (4.5) этой формы в базисе е является симметричной (кососимметричной). Справедливо и обратное – если матрица (4.5) билинейной формы  симметрична (кососимметрична), то и билинейная форма является симметричной (кососимметричной).
симметрична (кососимметрична), то и билинейная форма является симметричной (кососимметричной).
Пример 3 Рассмотрим линейное пространство 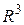 . Пусть
. Пусть 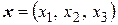 ,
, 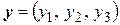 . Определим билинейную функцию
. Определим билинейную функцию  следующим образом:
следующим образом:  . Определим матрицу этой билинейной функции в базисе
. Определим матрицу этой билинейной функции в базисе 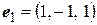 ,
, 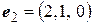 ,
, 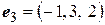 .
.
Так как размерность линейного пространства 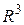 равна 3, то порядок матрицы билинейной функции
равна 3, то порядок матрицы билинейной функции  в базисе
в базисе 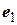 ,
, 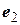 ,
, 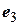 равна 3. Вычислим элементы матрицы:
равна 3. Вычислим элементы матрицы:
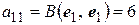 ,
, 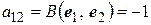 ,
,  ,
,
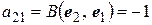 ,
, 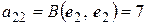 ,
, 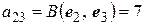 ,
,
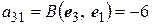 ,
, 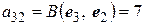 ,
, 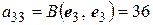 ,
,
Тогда матрица билинейной функции  в базисе
в базисе 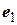 ,
, 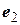 ,
, 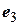 равна
равна
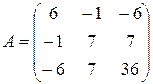 .
.
Выясним вопрос о преобразовании матрицы 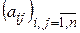 билинейной формы при переходе от базиса е к новому базису f.
билинейной формы при переходе от базиса е к новому базису f.
Справедливо следующее утверждение.
Теорема 4.2 Матрицы 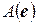 и
и 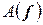 билинейной формы
билинейной формы 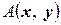 в базисах
в базисах 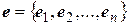 и
и 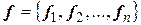 связаны соотношением
связаны соотношением
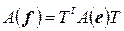 , (4.7)
, (4.7)
где  – матрица перехода от базиса е к базису
– матрица перехода от базиса е к базису 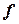 .
.
Пример 4 Дана матрица билинейной функции 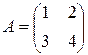 в базисе
в базисе 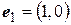 ,
, 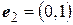 . Найти матрицу этой билинейной функции в базисе
. Найти матрицу этой билинейной функции в базисе 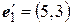 ,
, 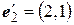 .
.
Матрица перехода имеет вид:  . Отсюда
. Отсюда 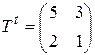 . Тогда матрица билинейной функции в базисе
. Тогда матрица билинейной функции в базисе 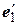 ,
, 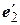 равна
равна 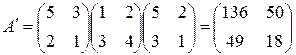 .
.
Следствие. Ранг матрицы 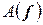 равен рангу матрицы
равен рангу матрицы 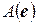 . Это сразу вытекает из соотношения (4.7), из того, что матрица
. Это сразу вытекает из соотношения (4.7), из того, что матрица 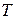 и, стало быть, матрица
и, стало быть, матрица 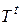 являются невырожденными, и из теоремы о том, что ранг матрицы не изменяется при умножении ее на невырожденную матрицу.
являются невырожденными, и из теоремы о том, что ранг матрицы не изменяется при умножении ее на невырожденную матрицу.
Это следствие позволяет ввести важный числовой инвариант билинейной формы – так называемый ранг билинейной формы.
Рангом билинейной формы, заданной в конечномерном линейном пространстве  , называется ранг матрицы этой формы в произвольном базисе пространства
, называется ранг матрицы этой формы в произвольном базисе пространства  .
.
Билинейная форма  , заданная в конечномерном линейном пространстве
, заданная в конечномерном линейном пространстве  , называется невырожденной (вырожденной), если ее ранг равен (меньше) размерности пространства
, называется невырожденной (вырожденной), если ее ранг равен (меньше) размерности пространства  .
.
Date: 2015-08-24; view: 2483; Нарушение авторских прав