Унитарный (ортогональный) оператор

Линейный оператор 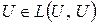() называется унитарным (ортогональным), если справедливо соотношение

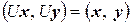. (3.16)

В дальнейшем соотношение (3.16) будем называть условием унитарности оператора.

Замечание 1 Из условия (3.16) унитарности оператора следует, что для любого унитарного оператора U справедливо равенство .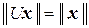

Отметим следующее утверждение.

Теорема 3.12 Если λ – собственное значение унитарного оператора U, то .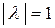

Теорема 3.13 Для того чтобы линейный оператор U, действующий в евклидовом пространстве 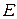, был унитарным, необходимо и достаточно, чтобы было выполнено соотношение

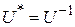. (3.17)

Замечание 2 В процессе доказательства теоремы установлено, что условие (3.16) унитарности оператора U и условие

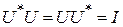(3.18)

эквивалентны. Таким образом, в основу определения унитарного оператора можно положить условие (3.18). Это условие также можно называть условием унитарности оператора U.

Матрица U называется ортогональной, если

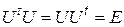. (3.19)

Если 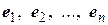– ортонормированный базис в евклидовом пространстве 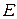, то оператор U является ортогональным тогда и только тогда, когда его матрица в базисе 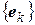ортогональна.

Свойства ортогональных матриц:

1. Действительная квадратная матрица ортогональна тогда и только тогда, когда выполняется хотя бы одно из равенств , .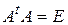

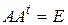2. Единичная матрица является ортогональной. Нулевая матрица ортогональной не является.

3. Если матрица ортогональна, то 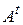тоже ортогональна.

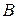4. Если матрицы и ортогональны, то 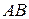– ортогональна.

5. Определитель ортогональной матрицы равен 1 или –1.

6. Действительная квадратная матрица ортогональна тогда и только тогда, когда все ее строки (столбцы) образуют ортонормированный базис в .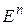

7. Матрица перехода от ортонормированного базиса к ортонормированному базису является ортогональной.

8. Если матрица перехода от одного базиса к другому ортогональна и один из этих базисов ортонормирован, то и второй базис является ортонормированным.

Непосредственно из равенства (3.19) следует, что если матрица 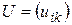является ортогональной, то

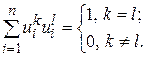
В заключение рассмотрим для примера ортогональных преобразований в одномерном и двумерном пространствах.

В одномерном случае каждый вектор имеет вид , где α – вещественное число, и е – вектор, порождающий данное пространство. Тогда , и так как 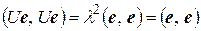, то .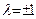

Таким образом, в одномерном случае существуют два ортогональных преобразования: 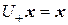и .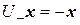

В двумерном случае каждое ортогональное преобразование определяется в произвольном ортонормированном базисе ортогональной матрицей второго порядка, т.е. матрицей 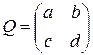. Из условия (3.18) следует

, , , , .

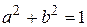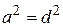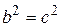Полагая , , 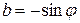получаем, что каждая ортогональная матрица второго порядка имеет вид

,

причем во второй строке в обоих случаях следует брать либо знак +, либо знак –.

Отметим, что . Ортогональная матрица называется собственной, а ортогональная матрица 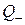– несобственной.

Оператор с матрицей в ортонормированном базисе 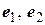осуществляет поворот в плоскости 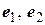на угол φ.

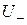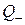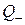Для того чтобы выяснить, как действует оператор с матрицей , введем матрицу , совпадающую с при 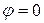, и заметим, что 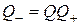. Матрице Q отвечает отражение плоскости относительно оси 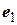, и следовательно, действие оператора заключается в повороте на угол φ и последующем отражении.

В общем случае, когда ортогональный оператор 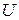действует в 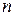-мерном евклидовом пространстве, существует ортонормированный базису, 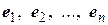, в котором матрица оператора Q имеет вид

.

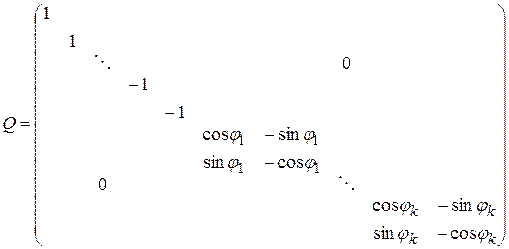В этой матрице все элементы, кроме выписанных, равны нулю.

Таким образом, в некотором ортонормированном базисе действие ортогонального оператора сводится к последовательным поворотам и отражениям относительно координатных осей.

Пример 10 Для ортогонального оператора, заданного в некотором ортонормированном базисе матрицей 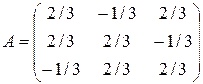, определить канонический вид и ортонормированный базис, в котором матрица ортогонального оператора имеет канонический вид.

Решение. В трехмерном евклидовом пространстве матрица ортогонального оператора в подходящем ортонормированном базисе имеет один из следующих видов:

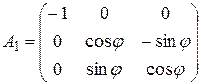и .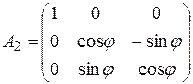

След матрицы линейного оператора – это инвариант линейного оператора, который не зависит от базиса.

Для матрицы : .

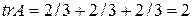Для матрицы : .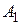

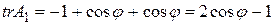Для матрицы : .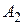

Равенство 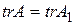невозможно, поэтому канонический вид матрицы ортогонального оператора равен .

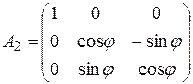Так как , то 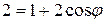. Отсюда и 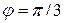. Поэтому

.

Собственные значения матриц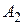ы равны 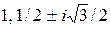. Найдем соответствующие собственные векторы.

Пусть 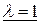. Тогда

Собственный вектор, соответствующий 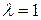, равен .

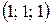Пусть . Тогда

.

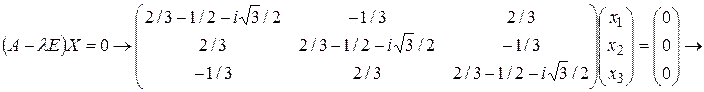
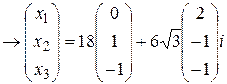Так как у нас действительное линейное пространство, то возьмем за два других собственных вектора действительную и мнимую части полученного вектора, т.е. 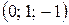и .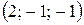

Базис из собственных векторов является ортогональным, получим из него ортонормированный базис:

, , .

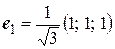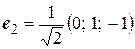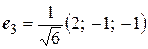Пример 11 Является ли унитарным оператор 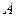, действующий в этом унитарном пространстве 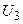, если в некотором ортонормированном базисе он имеет матрицу:

а) 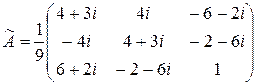; б) ?

Решение.

а) 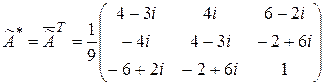. Проверим выполнение условия 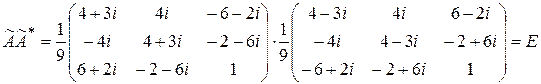. Значит, 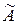– унитарная матрица, и, следовательно, – унитарный оператор.

б) 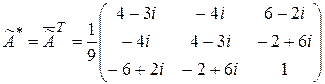. Проверим выполнение условия 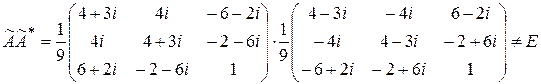. Значит, 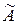не является унитарной матрицей, и, следовательно, не является унитарным оператором.

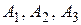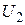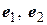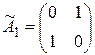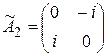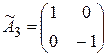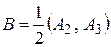Пример 12 Линейные операторы , действующие в этом унитарном пространстве , имеют в ортонормированном базисе матрицы: , , . Установить, являются ли операторы и унитарными операторами.

Решение. Так как 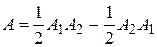, то матрица 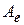этого оператора в базисе 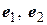имеет вид:

, ,

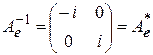значит, 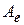– унитарная матрица. Поэтому – унитарный оператор.

Аналогично, матрица оператора в базисе 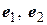имеет вид:

.

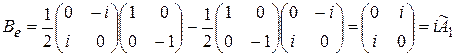Легко проверить, что условие унитарности выполняется, значит, 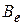– унитарная матрица. Поэтому 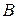– унитарный оператор.

3.4 Нормальный оператор

Линейный оператор А называется нормальным, если справедливо соотношение

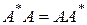. (3.19)

Обращаясь к условию (3.18) унитарности оператора и к условию (3.19), мы видим, что любой унитарный оператор является нормальным оператором.

Лемма. Пусть А – нормальный оператор. Тогда оператор А и оператор имеют общий собственный вектор 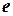такой, что 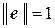, и справедливы соотношения и .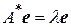

Теорема 3.14 Пусть А – нормальный оператор. Тогда существует ортонормированный базис 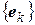, состоящий из собственных векторов операторов А и .

Следствие 1 Пусть А – нормальный оператор. Существует базис 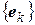, в котором А имеет диагональную матрицу.

Следствие 2 Унитарный оператор имеет полную ортонормированную систему собственных векторов.

Следующая теорема является обратной для теоремы 3.14.

Теорема 3.15 Если у действующего в 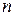-мерном евклидовом пространстве 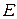оператора А имеется 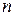попарно ортогональных собственных элементов 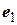, , 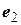…, , то оператор А нормальный.

Пример 13 Является ли нормальным линейный оператор, заданный в некотором ортонормированном базисе матрицей 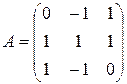? Если да, то найти канонический базис, т.е. ортонормированный базис, в котором матрица этого оператора имеет блочно-диагональный вид с блоками порядка 1 или 2.

Решение. Достаточно проверить равенство :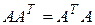

,

.

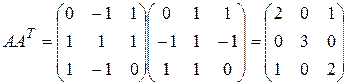Получили одинаковые матрицы, значит, оператор является нормальным.

Перейдем к поиску ортонормированного базиса. Найдем характеристический многочлен и его корни:

.

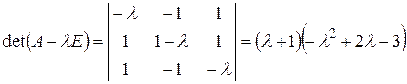Таким образом, 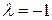, 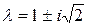. Найдем собственный вектор, соответствующий единственному действительному собственному значению :

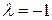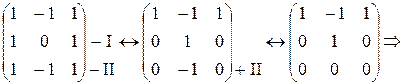
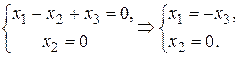
В этом случае собственный вектор .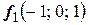

Найдем собственный вектор, соответствующий одному из двух сопряженных комплексных собственных значений, например, :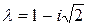

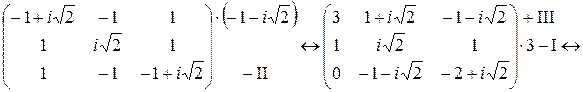
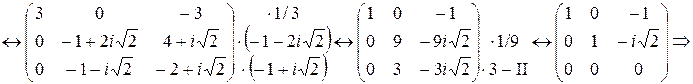
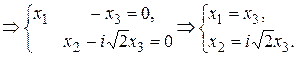
За собственные векторы возьмем действительную и мнимую части ФСР системы: , .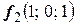

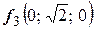Нормируя все найденные векторы, получим:

, ,

.

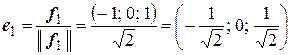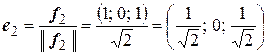Это и есть искомый ортонормированный базис. Так как

, , ,

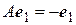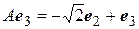то в этом ортонормированном базисе нормальный оператор 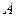имеет матрицу: .

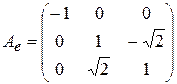Date: 2015-08-24; view: 3909; Нарушение авторских прав